Table 3. Root jumping in Newton Raphson method

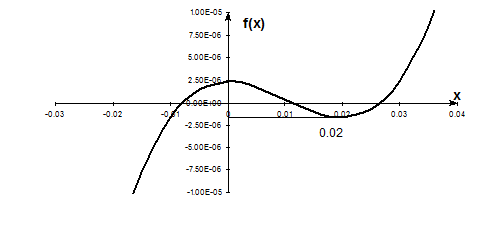
Figure 4. Pitfall of division by zero or a near zero number.

Table 2. Division by near zero in Newton Raphson method

Iteration Number	xi		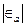f(xi)
	0.019990 -2.6480 -1.7620 -1.1714 -0.77765 -0.51518 -0.34025 -0.22369 -0.14608 -0.094490	100.75 50.282 50.422 50.632 50.946 51.413 52.107 53.127 54.602	-1.6000 x 10^-6 -18.778 -5.5638 -1.6485 -0.48842 -0.14470 -0.042862 -0.012692 -0.0037553 -0.0011091

2. Root jumping: In some case where the function f(x) is oscillating and has a number of roots, one may choose an initial guess close to a root. However, the guesses may jump and converge to some other root. For example for solving the equation 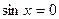if you choose 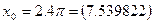as an initial guess, it converges to the root of x=0 as shown in Table 3. However, one may have chosen this an initial guess to converge to .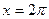

3.

Iteration Number		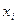f(xi)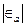
5	7.539822 4.461 0.5499 -0.06303 6.376x10^-4 -1.95861x10^-13	0.951 -0.969 0.5226 -0.06303 8.375x10^-4 -1.95861x10^-13	68.973 711.44 971.91 7.54x10^4 4.27x10^10

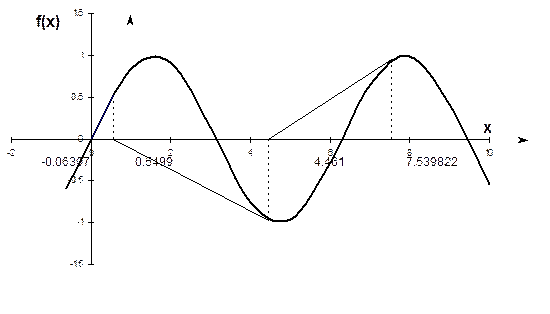Figure 5. Root jumping from intended location of root for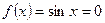
Oscillations near local maximum and minimum: Results obtained from Newton-Raphson method may oscillate about the local maximum or minimum without converging on a root but converging on the local maximum or minimum. Eventually, it may lead to division to a number close to zero and may diverge.

For example, for

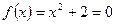
the equation has no real roots

Дата добавления: 2014-12-27