Закон полного тока для магнитного поля в веществе

Намагниченность

Для количественного описания намагничения магнетиков вводят векторную величину – намагниченность, определяемую магнитным моментом единицы объёма магнетика:

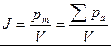, где

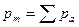– магнитный момент магнетика, представляющий собой векторную сумму магнитных моментов отдельных молекул.

Магнитное поле в веществе складывается из двух полей: внешнего поля, создаваемого током, и поля, создаваемого намагниченным веществом, тогда:

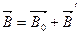, где

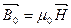– поле, создаваемое намагничивающим током в вакууме

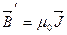– поле, создаваемое молекулярными токами

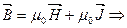
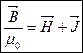
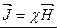, где

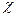– магнитная восприимчивость вещества (безразмерная величина)

Для диамагнетиков 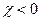, для парамагнетиков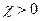

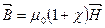
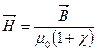
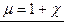– магнитная проницаемость (безразмерная величина), => 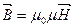– в среде.

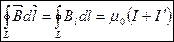, где

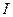и 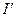– соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L.

Циркуляция вектора магнитной индукции 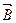по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Вектор 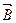характеризует результирующее поле, созданное как макроскопическими токами в проводниках (токами проводимости), так и микроскопическими токами в магнитиках, поэтому линии вектора магнитной индукции 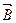не имеют источников и являются замкнутыми.

Докажем, что циркуляция намагниченности 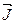по произвольному замкнутому контуру L равна алгебраической сумме молекулярных токов, охватываемых этим контуром:

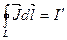
Тогда закон полного тока для магнитного поля в веществе запишем в виде:

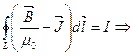
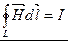– теорема о циркуляции вектора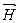

Циркуляция вектора 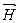по произвольному замкнутому контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром.

Раздел VII. Колебания и волны

Дата добавления: 2015-04-24