Энтропия и обратимость

Термодинамическая энтропия — термодинамическая функция, характеризующая меру неупорядоченности термодинамической системы, то есть неоднородность расположения и движения ее частиц.

Энтропия. Энтропия в обратимых и необратимых адиабатических процессах. Второе начало термодинамики.

• Энтропи́я (от греч. ἐντροπία — поворот, превращение) в естественных науках — мера беспорядка системы, состоящей из многих элементов. В частности, в статистической физике — мера вероятности осуществления какого-либо макроскопического состояния; в теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит и количество информации; в исторической науке, для экспликации феноменаальтернативности истории (инвариантности и вариативности исторического процесса).
• Энтропия в информатике — степень неполноты, неопределённости знаний.
• Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной приобратимых процессах, тогда как в необратимых — её изменение всегда положительно.
• ,
• где dS — приращение энтропии; δ Q — минимальная теплота, подведенная к системе; T — абсолютная температура процесса;

В общем случае для произвольной физической системы изменение состояния при адиабатическом расширении определяется производными термодинамических параметров при постоянной энтропии. Справедливы соотношения

,

,

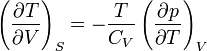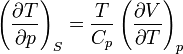где C_p и C_v — теплоёмкости при постоянном давлении и объёме, которые всегда положительны по своему физическому смыслу, 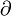— обозначение частной производной. Как и при определении молярной теплоёмкости, при расчёте частной производной находится изменения параметра в числителе, которое происходят только под действием изменения параметра, стоящего в знаменателе. Пусть система адиабатически расширяется, то есть Δ p < 0. Тогда если коэффициент теплового расширения 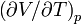положительный, изменение температурыΔ T должно быть отрицательным. То есть, температура системы будет уменьшатся при адиабатическом расширении, если коэффициент теплового расширения положителен, и увеличиваться в противоположном случае^[19]. Примером подобного процесса является эффект Джоуля — Томсона, который также является необратимым адиабатическим процессом^[20].

Необратимость адиабатических процессов связана с неравновесным переходом от начального состояния к конечному: система не следует адиабате Пуассона 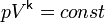, поэтому точный путь системы в координатах термодинамичесих величин не может быть указан. К необратимости может привести наличие внутреннего трения в газе, которое изменит энтропию системы. Так как выделяемое при изменении энтропии тепло не покидает систему (отсутствие обмена теплом с окружающей средой может быть навязано помещением системы в термостат), меняется температура газа. Изменение энтропии необратимого процесса из состояния A в состояние B можно расчитать соединив их на диаграмме несколькими отрезками путей, соответствующих обратимым процессам. Примерами необратимых адиабатических процессов являются дросселирование и смешение двух газов, первоначально находившихся при разных температурах и давлениях внутри поделённого пополам термостата

Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.

Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не должна равняться 0.

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

Дата добавления: 2015-04-24