Агрегатные состояния вещества

Распределение молекул по энергиям (Распределение Больцмана).

Распределение Больцмана

Главная Глоссарий Математические вычисления и доказательства

Это распределение по энергиям частиц (атомов, молекул) идеального газа в условиях термодинамического равновесия. Распределение Больцмана было открыто в 1868 - 1871 гг. австралийским физиком Л. Больцманом. Согласно распределению, число частиц n_i с полной энергией E_i равно:

n_i =A•ω_i •e^­E_i ^/Kt (1)

где ω_i - статистический вес (число возможных состояний частицы с энергией e_i). Постоянная А находится из условия, что сумма n_i по всем возможным значениям i равна заданному полному числу частиц N в системе (условие нормировки):

В случае, когда движение частиц подчиняется классической механике, энергию E_i можно считать состоящей из кинетической энергии E_iкин частицы (молекулы или атома), её внутренней энергии E_iвн (напр., энергии возбуждения электронов) и потенциальной энергии E_i,_пот во внешнем поле, зависящей от положения частицы в пространстве:

E_i = E_{i, кин} + E _{i, вн} + E_{i, пот} (2)

Распределение частиц по скоростям является частным случаем распределения Больцмана. Оно имеет место, когда можно пренебречь внутренней энергией возбуждения

E_i,вн и влиянием внешних полей E_i,пот. В соответствии с (2) формулу (1) можно представить в виде произведения трёх экспонент, каждая из которых даёт распределение частиц по одному виду энергии.

В постоянном поле тяжести, создающем ускорение g, для частиц атмосферных газов вблизи поверхности Земли (или др. планет) потенциальная энергия пропорциональна их массе m и высоте H над поверхностью, т.е. E_{i, пот} = mgH. После подстановки этого значения в распределение Больцмана и суммирования по всевозможным значениям кинетической и внутренней энергий частиц получается барометрическая формула, выражающая закон уменьшения плотности атмосферы с высотой.

В астрофизике, особенно в теории звёздных спектров, распределение Больцмана часто используется для определения относительной заселённости электронами различныхуровней энергии атомов. Если обозначить индексами 1 и 2 два энергетических состояния атома, то из распределения следует:

n₂/n₁ = (ω₂/ω₁)•e^-(E₂^-E₁^)/kT (3) (ф-ла Больцмана).

Разность энергий E₂-E₁ для двух нижних уровней энергии атома водорода >10 эВ, а значение kT, характеризующее энергию теплового движения частиц для атмосфер звёзд типа Солнца, составляет всего лишь 0,3-1 эВ. Поэтому водород в таких звёздных атмосферах находится в невозбуждённом состоянии. Так, в атмосферах звёзд, имеющихэффективную температуру Тэ > 5700 К (Солнце и др. звёзды), отношение чисел атомов водорода во втором и основном состояниях равно 4,2•10^-9.

Распределение Больцмана было получено в рамках классической статистики. В 1924-26 гг. была создана квантовая статистика. Она привела к открытию распределений Бозе - Эйнштейна (для частиц с целым спином) и Ферми - Дирака (для частиц с полуцелым спином). Оба эти распределения переходят в распределение, когда среднее число доступных для системы квантовых состояний значительно превышает число частиц в системе, т. о. когда на одну частицу приходится много квантовых состояний или, др. словами, когда степень заполнения квантовых состояний мала. Условие применимости распределении Больцмана можно записать в виде неравенства:

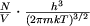где N - число частиц, V - объём системы. Это неравенство выполняется при высокой темп-ре и малом числе частиц в ед. объёма (N/V). Из этого следует, что чем больше масса частиц, тем для более широкого интервала изменений Т и N/V справедливо распределение Больцмана..

Агрега́тное состоя́ние — состояние вещества, характеризующееся определёнными качественными свойствами: способностью или неспособностью сохранять объём и форму, наличием или отсутствием дальнего и ближнего порядка и другими. Изменение агрегатного состояния может сопровождаться скачкообразным изменением свободной энергии, энтропии, плотности и других основных физических свойств.^[1].

Выделяют три основных агрегатных состояния: твёрдое тело, жидкость и газ. Иногда не совсем корректно к агрегатным состояниям причисляют плазму. Существуют и другие агрегатные состояния, например, жидкие кристаллы или конденсат Бозе — Эйнштейна.

Изменения агрегатного состояния это термодинамические процессы, называемые фазовыми переходами. Выделяют следующие их разновидности: из твёрдого в жидкое — плавление; из жидкого в газообразное — испарение и кипение; из твёрдого в газообразное — сублимация; из газообразного в жидкое или твёрдое — конденсация; из жидкого в твёрдое — кристаллизация. Отличительной особенностью является отсутствие резкой границы перехода к плазменному состоянию.

Определения агрегатных состояний не всегда являются строгими. Так, существуют аморфные тела, сохраняющие структуру жидкости и обладающие небольшой текучестью и способностью сохранять форму; жидкие кристаллы текучи, но при этом обладают некоторыми свойствами твёрдых тел, в частности, могут поляризовать проходящее через них электромагнитное излучение.

Для описания различных состояний в физике используется более широкое понятие термодинамической фазы. Явления, описывающие переходы от одной фазы к другой, называюткритическими явлениями.

[править]Твёрдое тело

Основная статья: Твёрдое тело

Состояние, характеризующееся способностью сохранять объём и форму. Атомы твёрдого тела совершают лишь небольшие колебания вокруг состояния равновесия. Присутствует как дальний, так и ближний порядок.

[править]Жидкость

Основная статья: Жидкость

Состояние вещества, при котором оно обладает малой сжимаемостью, то есть хорошо сохраняет объём, однако не способно сохранять форму. Жидкость легко принимает форму сосуда, в который она помещена. Атомы или молекулы жидкости совершают колебания вблизи состояния равновесия, запертые другими атомами, и часто перескакивают на другие свободные места. Присутствует только ближний порядок.

[править]Газ

Основная статья: Газ

Состояние, характеризующееся хорошей сжимаемостью, отсутствием способности сохранять как объём, так и форму. Газ стремится занять весь объём, ему предоставленный. Атомы или молекулы газа ведут себя относительно свободно, расстояния между ними гораздо больше их размеров.

[править]Плазма

Основная статья: Плазма

Часто причисляемая к агрегатным состояниям вещества плазма отличается от газа большой степенью ионизации атомов. Большая часть барионноговещества (по массе ок. 99,9 %) во Вселенной находится в состоянии плазмы.^[2]

[править]Сверхкритический флюид

Основная статья: Сверхкритический флюид

Возникает при одновременном повышении температуры и давления до критической точки, в которой плотность газа сравнивается с плотностью жидкости; при этом исчезает граница между жидкой и газообразной фазами. Сверхкритический флюид отличается исключительно высокой растворяющей способностью.

[править]Конденсат Бозе — Эйнштейна

Основная статья: Конденсат Бозе — Эйнштейна

Получается в результате охлаждения бозе-газа до температур, близких к абсолютному нулю. В результате этого часть атомов оказывается в состоянии со строго нулевой энергией (то есть в низшем из возможных квантовом состоянии). Конденсат Бозе — Эйнштейна проявляет ряд квантовых свойств, таких как сверхтекучесть и резонанс Фишбаха.

[править]Фермионный конденсат

Основная статья: Фермионный конденсат

Представляет собой Бозе-конденсацию в режиме БКШ «атомных куперовских пар» в газах состоящих из атомов-фермионов. (В отличие от традиционного режима бозе-эйнштейновской конденсации составных бозонов).

Такие фермионные атомные конденсаты являются «родственниками» сверхпроводников, но с критической температурой порядка комнатной и выше. ^[3]

[править]Вырожденная материя

§ Ферми-газ 1-я стадия Электронно-вырожденный газ, наблюдается в белых карликах, играет важную роль в эволюции звёзд.

§ 2-я стадия нейтронное состояние в него вещество переходит при сверхвысоком давлении, недостижимом пока в лаборатории, но существующем внутри нейтронных звёзд. При переходе в нейтронное состояние электроны вещества взаимодействуют с протонами и превращаются в нейтроны. В результате вещество в нейтронном состоянии полностью состоит из нейтронов и обладает плотностью порядка ядерной. Температура вещества при этом не должна быть слишком высока (в энергетическом эквиваленте не более сотни МэВ).

§ при сильном повышении температуры (сотни МэВ и выше) в нейтронном состоянии начинают рождаться и аннигилировать разнообразные мезоны. При дальнейшем повышении температуры происходит деконфайнмент, и вещество переходит в состояние кварк-глюонной плазмы. Оно состоит уже не из адронов, а из постоянно рождающихся и исчезающих кварков и глюонов. Возможно^[4], деконфайнмент происходит в два этапа.

§ При дальнейшем неограниченном повышении давления без повышения температуры вещество коллапсирует в чёрную дыру.

§ При одновременном повышении и давления, и температуры к кваркам и глюонам добавляются иные частицы. Что происходит с веществом, пространством и временем при температурах, близких к планковской, пока неизвестно.

[править]Другие состояния

При глубоком охлаждении некоторые (далеко не все) вещества переходят в сверхпроводящее или сверхтекучее состояние. Эти состояния, безусловно, являются отдельными термодинамическими фазами, однако их вряд ли стоит называть новыми агрегатными состояниями вещества в силу их неуниверсальности.

Неоднородные вещества типа паст, гелей, суспензий, аэрозолей и т. д., которые при определённых условиях демонстрируют свойства как твёрдых тел, так и жидкостей и даже газов, обычно относят к классу дисперсных материалов, а не к каким-либо конкретным агрегатным состояниям вещества.

24. Электрический заряд его свойства. Закон Кулона.

Электри́ческий заря́д — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие вэлектромагнитном взаимодействии. Впервые электрический заряд был введён в законе Кулона в 1785 году.

Заряд является количественной характеристикой. Единица измерения заряда в СИ — кулон — электрический заряд, проходящий через поперечное сечение проводника при силе тока 1 А за время 1 с. Заряд в один кулон очень велик. Если бы два носителя заряда (q1 = q2 = 1Кл) расположили в вакууме на расстоянии 1 м, то они взаимодействовали бы с силой 9×10⁹ H.

1.1.2.Свойства электрического заряда. Единица электрического заряда Кулон (Кл). В СИ эта единица производная. Заряд существует в двух видах. Тела, заряженные одноименным знаком отталкиваются, а разноименным притягиваются. Электрический заряд инвариантен. Его величина не зависит от системы отсчета, т.е. не зависит от того движется он или покоится. Электрический заряд дискретен. Заряд не может уменьшаться до бесконечно малого значения, Заряд любого тела представляет собой кратное от наименьшего электрического заряда – элементарного заряда. Электрический заряд аддитивен. Заряд системы тел (частиц) равен сумме зарядов тел (частиц), входящих в систему.

Зако́н Куло́на — это закон о взаимодействии точечных электрических зарядов.

Был открыт Шарлем Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона:

Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними

Иначе: Два точечных заряда в вакууме действуют друг на друга с силами, которые пропорциональны произведению модулей этих зарядов, обратно пропорциональны квадрату расстояния между ними и направлены вдоль прямой, соединяющей эти заряды. Эти силы называются электростатическими (кулоновскими).

Важно отметить, что для того, чтобы закон был верен, необходимы:

1. точечность зарядов — то есть расстояние между заряженными телами много больше их размеров — впрочем, можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;

2. их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;

3. взаимодействие в вакууме.

Однако с некоторыми корректировками закон справедлив также для взаимодействий зарядов в среде и для движущихся зарядов.^[1]

В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:

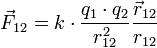
где — сила, с которой заряд 1 действует на заряд 2; q ₁, q ₂ — величина зарядов; 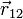— радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами — r ₁₂); k — коэффициент пропорциональности. Таким образом, закон указывает, что одноимённые заряды отталкиваются (а разноимённые — притягиваются).

25. Электростатическое поле, силовые линии, напряжённость, принцип суперпозиции.

Дата добавления: 2015-04-24