
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вывод основного уравнения МКТ. Для термодинамических систем выполняются законы термодинамики
Для термодинамических систем выполняются законы термодинамики.
Равновесные и неравновесные состояния и процессы. Всякая система может находиться в разных состояниях, отличается температурой, давлением и объёмом - это термодинамические параметры. Состояния бывают равновесными и неравновесными.
Равновесные состояния - это состояния, при которых все параметры системы имеют определённые значения, остающиеся при неизменных условиях одинаковыми.
Неравновесные состояния - это состояния, при которых какой-нибудь параметр изменяется. Процесс - это переход системы из одного состояния в другое. Равномерный процесс - это процесс состоящий из непрерывных состояний.
12. Среднеквадратичная скорость молекул. Молекулярно-кинетическое толкование абсолютной температуры.
Средняя квадратичная скорость молекул. Vср.кв.=Ö(3kT/M), где k=1,38×10-23 - постоянная Больцмана, T - температура.
Молекулярно-кинетическое толкование абсолютной температуры. С точки зрения молекулярно-кинетической теории абсолютная температура есть величина, пропорциональная средней энергии поступательного движения молекулы. <eпост>=3/2kT.
13. Основное уравнение молекулярно-кинетической теории (вывод). Число степеней свободы молекулы. Закон распределения энергии по степеням свободы. Внутренняя энергия идеального газа.
Пусть имеется кубический сосуд с ребром длиной l и одна частица массой m в нём.
Обозначим скорость движения vx, тогда перед столкновением со стенкой сосуда импульс частицы равен mvx, а после — − mvx, поэтому стенке передается импульс p = 2 mvx. Время, через которое частица сталкивается с одной и той же стенкой, равно 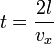 .
.
Отсюда следует: 
Так как давление  , следовательно сила F = p * S
, следовательно сила F = p * S
Подставив, получим: 
Преобразовав: 
Так как рассматривается кубический сосуд, то V = Sl
Отсюда: 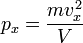 .
.
Соответственно, 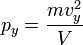 и
и 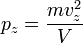 .
.
Таким образом, для большого числа частиц верно следующее: 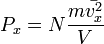 , аналогично для осей y и z.
, аналогично для осей y и z.
Поскольку 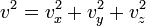 , то
, то 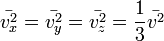 . Это следует из того, что все направления движения молекул в хаотичной среде равновероятны.
. Это следует из того, что все направления движения молекул в хаотичной среде равновероятны.
Отсюда 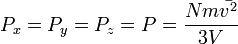
или 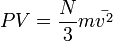 .
.
Пусть  — среднее значение кинетической энергии всех молекул, тогда:
— среднее значение кинетической энергии всех молекул, тогда: 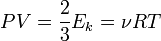 , откуда
, откуда 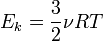 .
.
Для одного моля выражение примет вид 
Число степеней свободы молекулы. Число независимых координат, которые полностью определяют положение тела в пространстве, называется числом степеней свободы тела. Материальная точка имеет три степени свободы. Твёрдое тело произвольной формы - 6 (3 поступательных, три вращательных). 1. Одноатомная молекула - 3. 2. Двухатомная молекула - 5. 3. Трёхатомная молекула -7.
Закон распределения энергии по степеням свободы. На каждую степень свободы приходится в среднем одинаковая кинетическая энергия, равная 1/2kT. 1. Средняя энергия одной молекулы <e>=i(kT/2). 2. Внутренняя энергия одного моля газа. Um=<e>NA=(i/2)kNAT. 3. Внутренняя энергия произвольной массы газа. U=(m/M)UM=(m/M)(i/2)RT.
Внутренняя энергия идеального газа. U=N<e>, <e> - средняя кинетическая энергия молекул. <e>=(i/2)(kT), где k=1,38×10-23Дж/К, i - это сумма числа поступательных, вращательных и колебательных степеней свободы молекул. i=iпост.+ iвращ.+2iкол..
14. Работа газа при расширении. Количество теплоты. Первое начало термодинамики.
Работа газа при расширении. 1. Изобарный процесс. p=const, A=p(V2-V1). 2. Изотермический процесс. t=const, A=(m/M)RT×ln(V2/V1). 3. Адиабатный процесс. dQ=0 A=(m/M)Cv(T2-T1) или A=((m/M)(RT1)/(g-1))(1-(V1/V2)g-1).
Количество теплоты Q определяет количество энергии, переданной от тела к телу путём теплопередачи. Теплопередача - это совокупность микроскопических процессов, приводящих к передачи энергии от тела к телу. Q=U1-U2+A, где U1 и U2 - начальные и конечные значения внутренней энергии системы.
Первое начало термодинамики. Количество тепла, сообщённого системы идёт на приращение внутренней энергии системы и совершение работы над внешними телами. DQ=DU+DA. 1. При изобарном процессе Q=DU+A=nCvDT+nRDT. 2. При изохорном процессе A=0 Q=DU=nCvDT. 3. При изотермическом процессе DU=0 Q=A=nRDT×ln(V2/V1). 4. При адиабатном процессе Q=0 A=-DU=-nCvDT.
15. Классическая молекулярно-кинетическая теория теплоемкости. Удельная и молярная теплоемкости. Формула Майера. Границы применимости теории.
Классическая молекулярно-кинетическая теория теплоёмкости.
Теплоёмкостью какого либо тела называется величина равная количеству тепла, необходимого для того, чтобы изменить температуру тела на 1К. Cтела=dQ/dT (Джоуль/К). Теплоёмкость моля вещества называется молярной теплоёмкостью C (Джоуль/(Моль× К)).
Теплоёмкость единицы массы вещества называется удельной теплоёмкостью c (Джоуль/(кг×К)). c=C/M. Величина теплоёмкости зависит от условий, при которых происходит нагревание тела. 1. При постоянном объёме Cv=dU/dT. 2. При постоянном давлении:
|
где Δ V – изменение объема 1 моля идеального газа при изменении его температуры на Δ T. Отсюда следует:
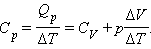
|
Отношение Δ V / Δ T может быть найдено из уравнения состояния идеального газа, записанного для 1 моля:
| pV = RT, |
где R – универсальная газовая постоянная. При p = const
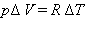 или или 
|
Таким образом, соотношение, выражающее связь между молярными теплоемкостями Cp и CV, имеет вид (формула Майера):
| Cp = CV + R. |
16. Изопроцессы идеального газа. Зависимость теплоемкости от вида процесса. Адиабатический процесс.
Изопроцессы идеального газа. У идеального газа есть три изопроцесса. 1. Изотермический процесс. T=const, pV=const, const=(m/M)RT. 2. Изобарный процесс. p=const, V/T=const, const=(m/M)R/p. 3. Изохорный процесс. V=const, p/T=const, const=(m/M)R/V.
Зависимость теплоёмкости от вида процесса. 1. Для изотермического процесса C=¥. 2. Для адиабатного процесса C=0.
Адиабатный процесс. Адиабатным называется процесс, протекающий без теплообмена с окружающей средой. Q=0 Þ газ при расширении совершает работ за счёт уменьшения его внутренней энергии. Þ газ охлаждается A'=DU. Кривая, изображающая адиабатический процесс называется адиабатой.
17. Тепловые двигатели и холодильные машины. КПД. Обратимые и необратимые процесы. Круговой процесс. Цикл Карно для идеального газа и его КПД.
Тепловой двигатель и холодильная машина. Тепловой двигатель это периодически действующий двигатель, совершающий работу за счёт поступающего из вне тепла. К.П.Д. тепловой машины это отношение совершённой работы за цикл к полученному теплу. Q1 - это количество получаемого тепла, Q2 это количество отдаваемого тепла. h=A/Q1=(Q1-Q2)/Q1, если обратить этот процесс, то получится цикл холодильной машины. Она отбирает за цикл от тела с температурой T2 количество теплоты Q2 и отдаёт телу с более высокой температурой T1 количество тепла Q1. К.П.Д. холодильной машины. Холодильный коэффициент=Q2/A'=Q2/(Q1'-Q2) - работа, которая затрачивается на приведение машины в действие.
К.П.Д. h=1-(T2/T1)=(T1-T)/T1 Коэффициент полезного действия всех обратимых машин, работающих в идентичных условиях, одинаков и определяется только температурами нагревателей и холодильников.
Обратимые и необратимы процессы. Обратимыми процессами называются такие процессы, которые могут быть проведены в обратном направлении таким образом, что система будет проходить через те же состояния, что и при прямом ходе, только в обратной последовательности. Необратимыми процессами называются такие процессы, которые не могут проходить в обратном направлении.
Круговой процесс. Круговыми процессами называются такие процессы, при которых система после ряда изменений возвращается в обратное состояние.
|
|
Дата добавления: 2015-04-24; Просмотров: 8709; Нарушение авторских прав?; Мы поможем в написании вашей работы!