Вопросы по молекулярной физике

Силы и потенциальная энергия межмолекулярного взаимодействия

Уравнение Ван-дер-Вальса описывает поведение газов в широком интервале плотностей: (p+(a'/V²))(V-b')=nRT, a'=n²a, b'=nb, где a и b - константы Ван-дер-Вальса, зависящие от газа, n - количество молей, p - давление, оказываемое на газ извне (равное давлению газа на стенки сосуда).

Изотермы реального газа. Изотермическое - это состояние, когда температура постоянна. Для этого случая, то есть для изотермической атмосферы зависимость давления от высоты равняется p=p₀exp(-(Mgh)/(RT)) - это барометрическая формула.

Внутренняя энергия реального газа. U=nC_vT-a'/V, где a'=n²a. По этой формуле можно находить приближенное значение внутренней энергии реальных газов.

http://physics-lectures.ru/

1. Идеальный газ. Уравнение состояния идеального газа.

Идеальным наз. газ у которого молекулы представляют из себя материальные точки и силы взаимодействия между ними возникают только при непосредственном взаимодействии (соударении) молекул. Давление р, температура Т и объем V, занимаемый определенной массой газа называются параметрами состояния. Каждый из параметров является функций двух других.

Уравнение, связывающее р, T и V для данной массы газа называется уравнением состояния. p = f (T,V)

Состояние газа однозначно определяется двумя любыми параметрами.
Основное уравнение кинетической теории газов p = n0kT n0 = N ⁄ V - концентрация, представим в виде: pV = NkT

Вместо неизмеряемого числа молекул газа N введем измеряемую величину - массу М газа.

Грамм- молекула (моль) вещества- такого количества вещества, масса которого в граммах равна молекулярной массе (μ), выраженной в частях массы молекулы углерода mc ⁄ 12.

Моль любого вещества содержит одинаковое количество молекул (по определению) - число Авогадро NA = 6,02 • 1023. Число молей вещества в данной массе равно:

N/N_A= M/μèN= M/μ*N_A - число молекул в данной массе газа.
Тогда основное кинетическое уравнение представим в форме

pV = M/μ NAkT

Произведение двух констант NA и k называется универсальной газовой постоянной.

R = NAk = 8,31 [Дж/к*моль] à 8,31 • 103 [Дж/к*моль]

Получим уравнение состояния идеального газа в форме Менделеева - Клайперона.

pV =M/μ RT

1. Давление идеального газа на основе молекулярно – кинетической теории.
2. Молекулярно – кинетическое толкование абсолютной температуры.

C точки зрения молекулярно-кинетической теории молекулы нагретого тела находятся в хаотическом движении. Причем, чем выше температура T, тем больше средняя кинетическая энергия <ε_k>хаотического движения молекул (T~<ε_k>).

Связь между средней кинетической энергией поступательного движения молекулы и абсолютной температурой дается формулой <ε_k>=3/2kT где k - постоянная Больцмана, k=1.38*10^-23 (Дж/К). Следовательно, абсолютная температура есть мера средней кинетической энергии поступательного движения молекулы.

Формула позволяет выяснить смысл абсолютного нуля: T=0, если < ε_k > =0. Т. е. абсолютный нуль - это температура, при которой прекращается всякое хаотическое движение молекул.

1. Число степени свободы молекул. Закон равномерного распространения энергии по степеням свободы молекул.

Числом степеней свободы механической системы называется число независимых координат, полностью определяющих положение системы в пространстве.

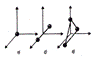показаны одноатомная, двухатомная и трехатомная молекулы. Одноатомную молекулу можно представить как материальную точку. Для определения положения точки в пространстве нужно три координаты, т. е. три степени свободы поступательного движения (i = 3). Молекулу двухатомного газа в первом приближении можно рассматривать как совокупность двух жестко связанных материальных точек. Эта молекула кроме трех степеней свободы поступательного движения имеет две степени свободы вращательного движения (i = 5). Вращение вокруг оси, проходящей через оба атома, не учитывается.

Трехатомная молекула с жесткими связями имеет 6 степеней свободы: 3 - поступательного и 3 - вращательного движения (i = 6).

В классической физике принят постулат о равномерном распределении энергии по степеням свободы. На каждую степень свободы любого вида движения приходится энергия, равная kT/2. Таким образом, средняя энергия одной молекулы равна <ε₁>=i/2kT В классической физике принят постулат о равномерном распределении энергии по степеням свободы. На каждую степень свободы любого вида движения приходится энергия, равная kT/2. Таким образом, средняя энергия одной молекулы равна <ε₁>=i/2kT

закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы - в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией потому, что на нее приходится не только кинетическая энергия, но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы <ε>=i/2kT, где i - сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы: i=i_пост +i_вращ+2i_колеб.

В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы.

Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю, то внутренняя энергия, отнесенная к одному молю газа, равна сумме кинетических энергий NA молекул: 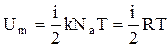.Внутренняя энергия для произвольной массы m газа 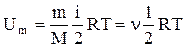, где k - постоянная Больцмана, n -количество вещества.

Функция распределения Максвела – Больцмона характеризует распределение молекул по полным энергиям

1. Закон Максвелла для распределения молекул идеального газа по скоростям.

Закон распределения молекул идеального газа по скоростям (закон Максвелла) определяет вероятное количество dN молекул из полного их числа N (число Авогадро) в данной массе газа, которые имеют при данной температуре Т скорости, заключенные в интервале от V до V + dV: dN/N=F(V)dV F(V) - функция распределения вероятности молекул газа по скоростям определяется по формуле; F(V)=4π(M/2πRT)^3/2 V² exp(MV²/2RT) где V - модуль скорости молекул, м/с; - абсолютная температура, градусы Кельвина, К;
М - молярная масса, кг/моль, численно равная молекулярной массе;
R = 8,3144 Дж/(моль•К) - универсальная газовая постоянная в системе СИ.

1. Закон Больцмана для распределения частиц во внешнем потенциальном поле.

1. Первое начало термодинамики.

Первое начало термодинамики представляет собой обобщение опытных фактов и является по сути дела законом сохранения энергии, примененным к тепловым явлениям. Первое начало термодинамики имеет несколько формулировок. Одна из формулировок гласит: количество теплоты, переданное системе, идет на изменение внутренней энергии и на совершение системой работы над внешними телами, т. е. Q=∆U+A В этом уравнении изменение внутренней энергии, Количество теплоты может быть положительным (Q>0), если тело получает теплоту, и отрицательным (Q>0), если тело отдает теплоту.

В дифференциальной форме это запишется следующим образом δQ=dU+δA

где dU и δA Первое начало термодинамики показывает, что теплоту можно преобразовывать в работу, т. е. выделять из неупорядоченного движения упорядоченное. Устройство, в котором теплота превращается в работу, называется тепловой машиной.

1. классическая молекулярно – кинетическая теория теплоемкости идеальных газов.

1. Первое начало термодинамики и изопроцессы.

Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.

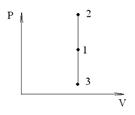Изохорный процесс (V=const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат, где процесс 1-2 есть изохорное нагревание, а 1-3 - изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т.е.

.δA=pdV=0

Для изохорного процесса следует, что вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии: dQ=dU

DUm=CvdT. Тогда для произвольной массы газа получим dQ=dU=mC_vT/M

Изобарный процесс (p=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, параллельной оси V. При изобарном процессе работа газа при расширении объема от V1 до V2 равна

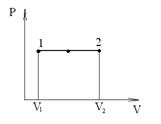
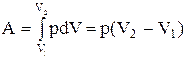и определяется площадью прямоугольника. Если использовать уравнение Клапейрона - Менделеева для выбранных нами двух состояний, то

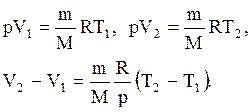
Тогда выражение для работы изобарного расширения примет вид

A=m/MR(T2-T1). Из этого выражения вытекает физический смысл молярной газовой постоянной R: если Т2-T1 =1 К, то для 1 моля газа R=А, т.е. R численно равна работе изобарного расширения 1 моля идеального газа при нагревании его на 1 К.

В изобарном процессе при сообщении газу массой m количества теплоты

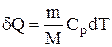его внутренняя энергия возрастает на величину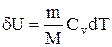

Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля - Мариотта: PV=const.

Диаграмма этого процесса (изотерма)в координатах р, V представляет собой гиперболу, расположенную на диаграмме тем выше, чем выше температура, при которой происходил процесс. Работа изотермического расширения газа:

.

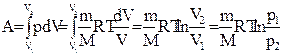Так как при T=const внутренняя энергия идеального газа не изменяется

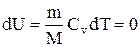то из первого начала термодинамики (dQ=dU+dA) следует, что для изотермического процесса dQ=dA, т.е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил 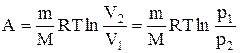Следовательно, для того, чтобы при работе расширения температура не уменьшалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.

1. Первое начало термодинамики и адиабатический процесс.

Адиабатическим называется процесс, при котором отсутствует теплообмен (dQ = 0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д. Из первого начала термодинамики d Q = dU + dA для адиабатического процесса следует, что d A = – dU * т. е. внешняя работа совершается за счет изменения внутренней энергии системы. Используя выражения для элементарной работы и приращения внутренней энергии, для произвольной массы газа получаем уравнение в виде pdV=-m/MC_vdT Продифференцировав уравнение состояния для идеального газа pV=m/MRT, получим pdV+Vdp=m/mRdT Исключив из уравнений температуру Т:

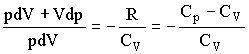
Разделив переменные и учитывая, что Cp/Cv = g, найдем dp/p=-γdV/V

Интегрируя это уравнение в пределах от р1 до р2 и соответственно от V1 до V2, а

затем потенцируя, придем к выражению p2/p1=(V₁/V₂) ^γ или p₁V₁^γ=p₂V₂^γ

Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

Для перехода к переменным Т, V или р, Т исключим из полученного уравнения с помощью уравнения Клапейрона -Менделеева

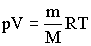соответственно давление или объем:TV^γ-1 = const T^γV^1-γ = const

Выражения представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина g = Cp/Cv = (i + 2)/I называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i = 3, g = 1,67. Для двухатомных газов (Н2, N2, О2 и др.) i=5, g =1,4. Значения g, вычисленные по формуле (g = (i + 2)/i), хорошо подтверждаются экспериментом.

Диаграмма адиабатического процесса (адиабата) в координатах р, V изображается гиперболой. На рисунке видно, что адиабата (pVg = const) более крутая, чем изотерма (pV=const). Это объясняется тем, что при адиабатическом сжатии 1 - 3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры в адиабатическом процессе. Запишем уравнение первое начало термодинамик для адиабатического процесса d A = – dU в виде

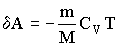Если газ адиабатически расширяется от объема Vl до V2, то его температура уменьшается от Т1 до Т2 и работа расширения идеального газа равна

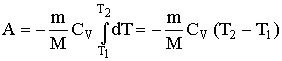
Работа, совершаемая газом при адиабатическом расширении 1 – 2 (численно равная площади под кривой), меньше, чем при изотермическом процессе. Это объясняется тем, что при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом – температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты

1. Явление переноса в термодинамически неравновесных системах. Опытные законы диффузии, теплопроводности и внутреннего трения(вязкости).

В термодинамически неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос энергии, массы, импульса. К явлениям переноса относятся теплопроводность (обусловлена переносом энергии), диффузия (обусловлена переносом массы) и внутреннее трение (обусловлено переносом импульса). 1.Теплопроводность. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит процесс выравнивания средних кинетических энергий молекул, т.е., иными словами, выравнивание температур.

Перенос энергии в форме теплоты подчиняется закону Фурье:

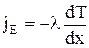,где J_E - плотность теплового потока – величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку перпендикулярную оси х, l - теплопроводность, dT/dx - градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что при теплопроводности энергия переносится в направлении убывания температуры Теплопроводность l численно равна плотности теплового потока при градиенте температуры равном единице.

Можно показать, что

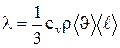,где сv - удельная теплоемкость газа при постоянном объеме, р - плотность газа, <υ> - средняя скорость теплового движения молекул, <ℓ> - средняя длина свободного пробега.

2. Диффузия. Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия сводится к обмену масс частиц этих тел, возникает и продолжается, пока существует градиент плотности. Во время становления молекулярно-кинетической теории по вопросу диффузии возникли противоречия. Так как молекулы движутся с огромными скоростями, диффузия должна происходить очень быстро. Если же открыть в комнате сосуд с пахучим веществом, то запах распространяется очень медленно. Однако противоречия здесь нет. Молекулы при атмосферном давлении обладают малой длиной свободного пробега и сталкиваясь с другими молекулами, в основном "стоят" на месте. Явление диффузии для химически однородного газа подчиняется закону Фика:

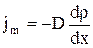, где j_m- плотность потока массы - величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х; D - диффузия (коэффициент диффузии); dp/dx - градиент плотности на единицу длины х в направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности Диффузия D численно равна плотности потока массы при градиенте плотности равном единице. Согласно кинетической теории газов,

.

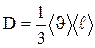3. Внутреннее трение (вязкость). Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее - увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее.

сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона: , где h - динамическая вязкость (вязкость), dυ/dx - градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев, S -площадь, на которую действует сила F. Взаимодействие двух слоев согласно второму закону Ньютона можно рассматривать как процесс, при котором от одного слоя к другому в единицу времени передается импульс, по модулю равный действующей силе. Тогда выражение (1.26) можно представить в виде 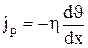, где j_p- плотность потока импульса – величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х; dυ/dx - градиент скорости. Знак минус указывает, что импульс переносится в направлении убывания скорости Динамическая вязкость h численно равна плотности потока импульса при градиенте скорости равном единице; она вычисляется по формуле

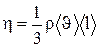. Из сопоставления формул описывающих явления переноса, следует, что закономерности всех явлений переноса сходны между собой. Из этих формул вытекают простые зависимости между l, D и h: h=rD, l/hcv=1.

1. Обратимые и не обратимые процессы. Энтропия. Второй закон термодинамики.

Второе начало термодинамики является фундаментальным законом природы. Оно охватывает самый широкий круг природных явлений и указывает направление, в котором самопроизвольно протекают термодинамические процессы.

Второе начало термодинамики, как и первое, имеет несколько формулировок.

Невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, полностью в работу.

Невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.

Эти формулировки показывают, что тепловые процессы являются необратимыми. Мерой необратимости процесса, мерой хаотичности является энтропия.

К определению энтропии S можно прийти на основе анализа работы тепловых машин. Если система получает тепло (Q>0) или отдает тепло (Q<0), то состояние ее меняется. Тогда, при изменении состояния системы, можно найти не саму энтропию, а только ее изменение, т. е. ∆S=∆Q/T

Для тепловой машины изменение энтропии нагревателя и холодильника равны: ∆S₁=Q₁/T₁ и ∆S₂=Q₂/T₂

Формула ∆S=∆Q/T справедлива для изотермического процесса и представляет собой термодинамическое определение энтропии. Энтропией называется термодинамическая величина, изменение которой в системе пропорционально ее тепловой энергии, деленной на абсолютную температуру. Для любого процесса можно найти бесконечно малое изменение энтропии, т. е. ее дифференциал dS=δQ/T, где δQ- элементарная теплота

В интегральной форме для любого процесса изменение энтропии равно

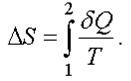Найдем изменение энтропии за один цикл для тепловой машины. Из неравенства следует, что ∆S₂≥∆S₁. Полное изменение энтропии за цикл больше или равно нулю ∆S=∆S₂-∆S₁≥0 Знак равенства ΔS = 0 относится к обратимым процессам, которые являются бесконечно медленными процессами.

Знак неравенства ΔS > 0 относится к необратимым процессам. В реальных системах все процессы необратимы. Например, расширение газа, выравнивание температуры.

Таким образом, второе начало термодинамики формулируется и как закон возрастания энтропии. Во всех необратимых процессах в замкнутой системе энтропия всегда возрастает. Возрастание энтропии сопровождается выравниванием температуры или плотности газа. Это можно связать с порядком и беспорядком. Под порядком будем понимать сосредоточение частиц или энергии в определенном месте пространства, а под беспорядком (хаосом) - равномерное распределение их во всем объеме. Тогда возрастание энтропии при совершающихся без внешних воздействий необратимых процессах отражает природное стремление систем переходить от состояния более упорядоченного в состояние менее упорядоченное. Этот процесс сопровождается рассеянием (или диссипацией) энергии. Второе начало термодинамики определяет направленность тепловых процессов в изолированных системах, они всегда протекают в сторону роста энтропии, в сторону увеличения беспорядка. Возникновение упорядоченных структур возможно только в незамкнутых, т. е. в открытых системах. Открытой системой называется система, которая обменивается энергией и веществом с окружающей средой. В открытых системах энтропия может как возрастать, так и убывать в зависимости от знака Q/T.

В открытых системах, находящихся в неравновесном состоянии, при определенных условиях из хаоса может возникать порядок. Процесс возникновения из хаоса упорядоченных структур называется самоорганизацией. Процессы самоорганизации являются общими для живой и неживой природы.

1. Тепловые двигатели. Цикл Карно и его КПД для идеального газа.

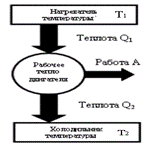Тепловые машины могут иметь разную конструкцию. Это может быть паровой двигатель, двигатель внутреннего сгорания, реактивный двигатель. Любой тепловой двигатель работает по замкнутому циклу и имеет нагреватель, рабочее тело двигателя и холодильник. В процессе работы теплового двигателя рабочее тело двигателя получает от нагревателя количество теплоты Q₁, совершает работу A и передает холодильнику количество теплоты Q₂<Q₁. Для замкнутого цикла изменение внутренней энергии равно нулю (∆U=0). Следовательно, согласно I началу термодинамики, работа, совершаемая двигателем, равна A=Q₁-Q₂ Коэффициентом полезного действия (КПД) теплового двигателя называется отношение работы, совершаемой двигателем, к количеству теплоты, полученному от нагревателя η=Q₁-Q₂/Q₁ КПД тепловой машины всегда меньше единицы η=1-Q₂/Q₁ Следовательно, невозможно всю теплоту превратить в работу. Ученые всегда стремились повысить КПД. В первой половине XIX в. французский ученый Сади Карно показал, что максимально возможное значение КПД тепловой машины равно η_max=T₁-T₂/T₁=1-T₂/T₁, где T ₁ - температура нагревателя, T ₂ - температура холодильника. Из сравнения уравнений (4.18) и (4.19) следует, что η_max ≥ η или 1-T₂/T₁≥1Q₂/Q₁. Отсюда Q₂/T₂≥Q₁/T₁ На основании этого неравенства можно прийти к понятию энтропия и второму началу термодинамики. Повышение КПД тепловых двигателей и приближение его к максимально возможному значению - важнейшая техническая задача. Однако, все тепловые двигатели выделяют большое количество теплоты, что называется тепловым загрязнением, и выбрасывают в атмосферу вредные для растений и животных химические соединения.

1. Энтропия и вероятность. Формула Больцмана.

Второе начало термодинамики является фундаментальным законом природы. Оно охватывает самый широкий круг природных явлений и указывает направление, в котором самопроизвольно протекают термодинамические процессы.

Второе начало термодинамики, как и первое, имеет несколько формулировок.

Невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, полностью в работу.

Невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.

Эти формулировки показывают, что тепловые процессы являются необратимыми. Мерой необратимости процесса, мерой хаотичности является энтропия.

К определению энтропии S можно прийти на основе анализа работы тепловых машин. Если система получает тепло (Q=0) или отдает тепло (Q<0), то состояние ее меняется. Тогда, при изменении состояния системы, можно найти не саму энтропию, а только ее изменение, т. е. ∆S=∆Q/T Для тепловой машины изменение энтропии нагревателя и холодильника равны: ∆S₁=Q₁/T₁ и ∆S₂=Q₂/T₂

Формула ∆S=∆Q/T справедлива для изотермического процесса и представляет собой термодинамическое определение энтропии. Энтропией называется термодинамическая величина, изменение которой в системе пропорционально ее тепловой энергии, деленной на абсолютную температуру. Для любого процесса можно найти бесконечно малое изменение энтропии, т. е. ее дифференциал dS=δQ/T

где δQ - элементарная теплота В интегральной форме для любого процесса изменение энтропии равно

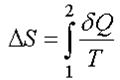Найдем изменение энтропии за один цикл для тепловой машины. Из неравенства следует, что ∆S₂≥∆S₁. Полное изменение энтропии за цикл больше или равно нулю ∆S=∆S₂-∆S₁≥0

Знак равенства ΔS = 0 относится к обратимым процессам, которые являются бесконечно медленными процессами.

Знак неравенства ΔS > 0 относится к необратимым процессам. В реальных системах все процессы необратимы. Например, расширение газа, выравнивание температуры.

Таким образом, второе начало термодинамики формулируется и как закон возрастания энтропии. Во всех необратимых процессах в замкнутой системе энтропия всегда возрастает. Возрастание энтропии сопровождается выравниванием температуры или плотности газа. Это можно связать с порядком и беспорядком. Под порядком будем понимать сосредоточение частиц или энергии в определенном месте пространства, а под беспорядком (хаосом) - равномерное распределение их во всем объеме. Тогда возрастание энтропии при совершающихся без внешних воздействий необратимых процессах отражает природное стремление систем переходить от состояния более упорядоченного в состояние менее упорядоченное. Этот процесс сопровождается рассеянием (или диссипацией) энергии. Второе начало термодинамики определяет направленность тепловых процессов в изолированных системах, они всегда протекают в сторону роста энтропии, в сторону увеличения беспорядка. Возникновение упорядоченных структур возможно только в незамкнутых, т. е. в открытых системах. Открытой системой называется система, которая обменивается энергией и веществом с окружающей средой. В открытых системах энтропия может как возрастать, так и убывать в зависимости от знака Q/T.

Строго доказано, что в открытых системах, находящихся в неравновесном состоянии, при определенных условиях из хаоса может возникать порядок. Процесс возникновения из хаоса упорядоченных структур называется самоорганизацией. Процессы самоорганизации являются общими для живой и неживой природы.

Переход к статистическому весу позволяет записать выражение для энтропии в следующем виде:

S=klnG Эта формула носит название формулы Больцмана. Она позволяет рассчитать статистическую энтропию системы.

Из этой формулы следует, что энтропия термодинамической системы со статистическим весом равным единице, когда все частицы системы находятся в одинаковых состояниях, равна нулю. А в состоянии с максимальным статистическим весом энтропия также принимает максимальное значение.

Для статистической энтропии выполняется требование аддитивности. Если система может быть разделена на две не взаимодействующие подсистемы, статистические веса которых соответственно равны G1и G2, то её статистический вес G вычисляется как произведение весов подсистем: G=G₁G₂. При этом энтропия в соответствии с формулой равна: S=klnG=kln(G1G2)=klnG1+klnG2 или S=S1+S2 Следовательно, статистическая энтропия макроскопической системы, состоящей из не взаимодействующих подсистем, равна сумме энтропий этих подсистем.

Дата добавления: 2015-04-24