Кванторные операции над предикатами

Вопрос №12. Логические операции над предикатами.

Коньюнкция, дизьюнкция, отрицание, импликация, эквивалентность

Коньюнкцией двух предикатов Р(х) и Q(x) называется новый предикат Р(х)&Q(x) который принимает значение истинно при тех и только тех значениях х€М при которых каждый из предикатов принимает значение истинна и ложь во всех остальных случаях

Область истинности Р(х)&Q(x) является Р+UQ+

Пример. P(x) «x – чётное число»

Q(х) «х –кратно 3»

Тогда предикат Р(х)&Q(x) можно записать следующим образом: «х делится на 6»

Р+UQ+ объединение.

Для остальных операций по анологии- так написано в лекциях.

Пусть имеется предикат Р(х), определённый на множестве М. Если а — некоторый элемент из множества М, то подстановка его вместо х в предикат Р(х) превращает этот предикат в высказывание Р(а). Такое высказывание называется единичным. Наряду с образованием из предикатов единичных высказываний в логике предикатов рассматривается ещё две операции, которые превращают одноместный предикат в высказывание.

1. Квантор всеобщности. Пусть Р(х) — предикат, определённый на множестве М. Под выражением 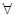хР(х) понимают высказывание, истинное, когда Р(х) истинно для каждого элемента х из множества М и ложное в противном случае. Это высказывание уже не зависит от х. Соответствующее ему словесное выражение будет «для всякого х Р(х) истинно». Символ 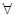называют квантором всеобщности.

Переменную х в предикате Р(х) называют свободной и ей можно придавать различные значения из М, а в высказывании 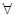xP(x) переменную х называют связанной квантором всеобщности ().

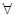2. Квантор существования. Пусть Р(х) — предикат, определённый на множестве М. Под выражением 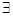хР(х) понимают высказывание, которое является истинным, если существует элемент х 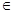М, для которого Р(х) истинно, и ложным в противном случае. Это высказывание уже не зависит от х. Соответствующее ему словесное выражение будет: «Существует х, при котором Р(х) истинно». Символ 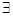называют квантором существования. В высказывании 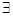х(х) переменная х связана квантором существования ().

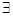Дата добавления: 2015-04-24