Логический квадрат

Примечание языка логики предикатов для записи математических предложений.

Алгоритмы распознавания общезначимости формул в частных случаях.

Формула А называется выполняемой области М если существует значения переменных при которых А принимает истинное значение.

А называется выполняемой если существует область на которой эта формула выполнима.

А называется ТИ в области М если принимает истинные значения для всех значений переменного (т е на все А называется общезначимой если она 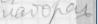ТИ на всякой области.

А ТЛ в области М если она принимает логичные значения для всех переменных.

Общезначимые формулы называются логическим законом.

Систему взаимоотношений между универсальными и экзистенциальными высказываниями возникающими при определении операций взятия квантора общности и квантора существования. Схематично представляют в виде логического квадрата

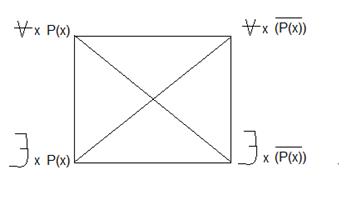
Высказывание 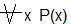и - не могут быть не для какого предиката Р(х) одновременно истинными (хотя могут быть одновременно ложными). Их называют контрарными.

Высказывание 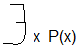и 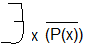не могут быть не для какого предиката Р(х) одновременно ложными (но могут быть одновременно истинными). Их называют субконтрарными.

Те высказывания, стоящие в вершинах каждой диагонали квадрата противоречат одно другому.

Под каждым из универсальных высказываний, стоящих в вершинах стоит высказывание следующего из него, то импликация этих высказываний являются истинной.

Дата добавления: 2015-04-24