Перевод чисел из произвольной системы счисления в десятичную

Основные понятия, используемые в двоичной системе счисления

Позиционная система счисления

В позиционных системах счисления, к которым относятся и широко распространенная десятичная система, числовое значение цифры зависит от ее местоположения или позиции в последовательности цифр изображающих число. Единственной, дошедшей до нашего времени, системой, не относящейся к позиционной системе счисления, является римская система счисления.

Любое число в позиционной системе счисления изображается последовательностью цифр:

Х = а_n-1 a_n-2…a₁a₀,

где a_iє{0,1,…,q-1}, q – основание системы счисления.

Наибольшее распространение получили системы счисления с основанием q=2, 8, 10, 16.

Если q >10, то вводят специальные символы, соответствующие цифрам 10, 11 и т.д. Так в 16-ной системе счисления такими символами являются начальные буквы латинского алфавита:

[А(10), В(11), С(12), D(13), E(14), F(15)].

Микропроцессорная техника оперирует двоичными цифрами. Независимо от изображения чисел и цифр в программе пользователя, микропроцессор всегда преобразует их в последовательность двоичных цифр: 0 и 1.

Обозначение основания системы счисления числа производится нижним числовым индексом после записи числа, либо передними символами:

(123₈, 123₁₀, 123₁₆,…) или 0х__(₁₆), bx__(₂).

Используют следующие сокращения для обозначения форматов двоичных чисел.

Бит – двоичная цифра, имеющая два значения (0, 1).

С помощью двух бит можно представить четыре числа (00, 01, 10, 11).

С помощью трех бит можно представить восемь чисел.

С помощью n бит можно представить 2ⁿ чисел.

Тетрада – это комбинация из четырех бит, она описывает 16 комбинаций чисел, т.е. совпадает с числом цифр в 16-теричной системе счисления. Т.о. любую комбинацию тетрады мы можем записать либо 4 битами, либо одной цифрой 16-ной системы счисления:

0000₂ = 0₁₆ 1000₂ = 8₁₆

0001₂ = 1₁₆ 1001₂ = 9₁₆

0010₂ = 2₁₆ 1010₂ = А₁₆

0011₂ = 3₁₆ 1011₂ = В₁₆

0100₂ = 4₁₆ 1100₂ = С₁₆

0101₂ = 5₁₆ 1101₂ = D₁₆

0110₂ = 6₁₆ 1110₂ = E₁₆

0111₂ = 7₁₆ 1111₂ = F₁₆

Байт (от английского слова “слог”) – это группа из 8 бит.

Байт позволяет описать 256 различных чисел. Биты в байте номеруются справа, налево начиная с нуля.

Самое младшее число в 16-теричной системе счисления, формата байт, записывается в виде 00₁₆, а самое старшее число записывается в виде FF₁₆.

Слово – это комбинация из 16 бит или 2 байт. Слово содержит:

2¹⁶ = 65536 комбинаций.

Для краткой записи больших степеней числа 2 (что используется при характеристике объема памяти) величину 2¹⁰ обозначают буквой К, которая читается “килобайт” (Кбайт), число 2²⁰ обозначают М, которая читается “мегабайт” (Мбайт), число 2³⁰ обозначают Г, которая читается “гигабайт” (Гбайт).

Десятичное значение числа, записанного в любой системе исчисления, определяется по формуле: ,

где - разряды исходного числа; 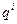- вес i-ого разряда; i – номер текущего разряда; n – число разрядов исходного числа.

Пример №1:

Определить десятичный эквивалент числа

Пример №2:

Определить десятичный эквивалент числа

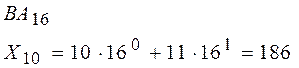
Дата добавления: 2015-04-24