Случаи приведения пространственной системы к простейшему виду

Коэффициент устойчивости.

Устойчивость тел при опрокидывании.

Случаи приведения плоской системы к простейшему виду.

Теорема об эквивалентности пар сил.

Моменты силы относительно оси.

Теорема о параллельном переносе сил.

Равновесие плоской системы параллельных сил.

Сложение параллельных сил и пар, направленных в разные стороны.

Сложение параллельных сил и пар, направленных в одну сторону.

Равнодействующие двух параллельных сил направленных в одну сторону, равна по модулю сумме слагаемых сил, им параллельна и направлена в туже сторону. R=F1+F2

Точка приложения равнодействующей делит расстояние между силами на части обратно пропорциональные приложенным.

Равнодействующие двух параллельных сил направленных в разные стороны, равна по модулю их разности и направлена в сторону большей силы. R=F1-F2

Приложенная R делит расстояние между силами на части, обратно пропорциональные приложенным силам.

16 Основные свойства пар сил:

1 пара сил равнодействующей не имеет.

2 пара сил стремится придать телу вращательный эффект.

3 сумма моментов сил пары относительно точки не зависит от выбора точки и всегда равняется моменту пары

В случае, когда все действующие на тело силы параллельны друг другу, мы можем направить ось Ох перпендикулярно к силам, а ось Оу параллельно им (рис. 29). Тогда проекция каждой из сил на Ox будет равна нулю и первое из 3-х равенств обратится в тождество вида 0 = 0.

Силу, приложенную к абсолютно твердому телу, можно не изменяя ее действия переносить в любую точку тела прибавляя пару сил, момент которой равен моменту переносимой силы относительно той точки, куда сила переносится.

Момент силы относительно оси равен алгебраическому моменту проекции этой силы на плоскость перпендикулярную оси, взятому относительно точки пересечения оси с этой плоскостью.

Пары сил, лежащие в одной плоскости, эквивалентны, если их моменты численно равны и одинаковы по знаку.

1 R=0, M0=0 - система сил в равновесии

2 R=0, M0=/0 - система сил приводится к одной паре сил с главным моментом, и плечо вращается

3 R=/0, M0=0 – система приводится к равнодействующей, проходящей через центр приведения(тело движется поступательно)

4 R=/0, Mo=/0 – система приводится к равнодействующей, не проходящей через центр приведения

Вытекает из условия равновесия рычага (EM0(Fn)=-P*h+G*a=0),это актуально для дымовых труб, башенных кранов.

Ga – момент удерживающий

Ph – момент опрокидывающий

Мудер.=Мопрак.

К=Мудер./Мопрак.

К=1 неустойчивое состояние

К>1 устойчивое

1,5<=К<=2 в технике

1. 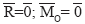– система уравновешена.
2. 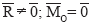– система приводится к равнодействующей, К проходит через «0»
3. 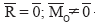– система приводится к паре сил.
4. – равнодействующая, но не проходящая через «0»;

совокупность равнодействующей и пары сил, лежащей в плоскости перпендикулярной силе;

динамический винт, ось винта не будет проходить через «0».

Дата добавления: 2015-03-29