Отрицание

Классификация моделей

Классифицировать модели можно по разным критериям. Например, по характеру решаемых проблем модели могут быть разделены на функциональные и структурные. В первом случае все величины, характеризующие явление или объект, выражаются количественно. При этом одни из них рассматриваются как независимые переменные, а другие — как функции от этих величин. Математическая модель обычно представляет собой систему уравнений разного типа (дифференциальных, алгебраических и т. д.), устанавливающих количественные зависимости между рассматриваемыми величинами. Во втором случае модель характеризует структуру сложного объекта, состоящего из отдельных частей, между которыми существуют определенные связи. Как правило, эти связи не поддаются количественному измерению. Для построения таких моделей удобно использовать теорию графов. Граф — это математический объект, представляющий собой некоторое множество точек (вершин) на плоскости или в пространстве, некоторые из которых соединены линиями (ребрами).

По характеру исходных данных и результатов предсказания модели могут быть разделены на детерминистические и вероятностно-статистические. Модели первого типа дают определенные, однозначные предсказания. Модели второго типа основаны на статистической информации, а предсказания, полученные с их помощью, имеют вероятностный характер.

1) 1. КОНЕЧНЫЕ УРАВНЕНИЯ КАК МАТЕМАТИЧЕСКИЕ МОДЕЛИ. ОСНОВНЫЕ МЕТОДЫ ИХ РЕШЕНИЯ И РЕАЛИЗАЦИЯ НА ЭВМ.

Уравнение, которое приводится к виду 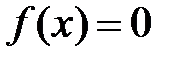, где 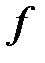‒ функция, называется конечным (в отличие, например, дифференциального или интегрального уравнения). Функция, находящаяся в левой части конечного уравнения может зависеть и от многих переменных.

Такие уравнения или их системы часто представляют математические модели или их компоненты при решениях прикладных задач, то есть таких, условия которых содержат нематематические понятия.

Химическая задача

Сколько атомов в молекуле серы при 1160°С, если плотность паров серы по воздуху при этой температуре равна 2,2?

Это прикладная задача: её условие содержит такие нематемати­ческие понятия как молекула, атомы, плотность паров и т. п.

Так как относительная молекулярная масса воздуха равна 29, то относительная молекулярная масса серы, соответствующая условию задачи, будет 29·2,2 = 63,8. Обозначив число атомов в молекуле серы через х, и, учитывая, что относительная атомная масса серы равна 32, для определения неизвестного, получим уравнение 32х= 63,8. Итак, составленное конечное (линейное) уравнение ‒ это математическая модель задачи. Решение этого уравне­ния должно принадлежать множеству натуральных чисел, поскольку количество атомов в молекуле ‒ число целое. Это замечание очень важное, так как все используемые количественные данные являются приближенными. Итак, ответ: х = 2, т. е. искомая молекула содержит 2 атома серы, S₂ ‒ её молекулярная формула. Найденное решение является добротным, устойчивым по отноше­нию к ошибкам измерений плотности паров серы: небольшие по­грешности не влияют на результат!

Действительно, пусть плотность равна 2,1 или 2,3, тогда пра­вая часть уравнения соответственно будет 29·2,1 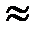61 или 29·2,3 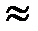67, но поскольку индекс в формуле серы ‒ натуральное число, то, рассуждая, как и выше, получим тот же результат.

Физическая задача

Камень бросили вертикально вверх с начальной скоростью 10 м/с. Через сколько времени он поднимется на высоту, равную 5,0 м?

В этих условиях сопротивлением воздуха будем пренебрегать,и ускорение свободного падения считать постоянным. Переход к математической модели задачи осуществляется так же, как и при решении любой текстовой задачи на составление уравнений, при этом каждый пользуется знаниями, полученными и по физике и по математике.

Итак, введём направленную вертикально вверх координат­ную ось у, начало которой совместим с камнем, моделируемым материальной точкой. При сделанных предположениях движение камня вдоль оси у будет определяться постоянным ускорением свободного падения g (м/с²) и начальной скоростью v₀ (м/с). В этих условиях, как известно из курса физики, характер движения камня описывается функцией

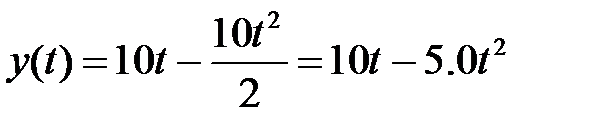
Теперь для решения сформулированной задачи обозначим через t с ‒ время, через которое камень окажется на высоте 5,0 м, тогда для определения t получим на основании (10.1) уравнение y(t) = 5,0 или 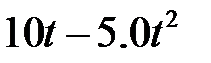=5,0, т.е.,

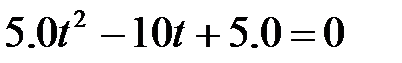, (1)

которое и является математической моделью рассматриваемой конкретной физической задачи. Этим завершается первый этап решения прикладной задачи средствами математики.

На втором этапе решаем уже математическую задачу, т.е. квадратное уравнение (1), в котором t ‒ неизвестное. Сначала найдём дискриминант D=0. Однако это равенство приближённое, о чём свидетельствует значение коэффициента 5,0 в уравнении (1).

Формально уравнение (1) имеет единственное решение t =1,0. Но здесь есть одно осложнение: малые погрешности в исходных данных могут существенно изменить решение и тогда оно оказывается недостоверным: при D < 0 его нет, а при D > 0 их два. Решение t = 1,0 ‒ неустойчиво. Здесь можно говорить об условной устойчивости, когда при малых погрешностях в исход­ных данных малым будет D > 0.

Неочевидные лишние данные задачи часто могут быть обнаружены с помощью ЭВМ, в особенности, если решение можно свести к перебору всех возможных вариантов, удовлетворяющих заданным условием. Для этого сначала составляет и реализуется на ЭВМ программа, использующая все исходные данные. Затем реализуется только части программы соответствующей задачи, из условия которой исключается те или иные сведения. Если при каком-то варианте исключения данных из непротиворечивой задачи получается тот же результат, что и при всей исходной информации, то такие данные без ущерба для дела можно отбросить и таким образом придать задаче более совершенную формулировку. Таким образом, используя ЭВМ, можно обнаружить в задачах лишние данные, если они имеются, и, исключив из, совершенствовать формулировки задач. Постановка задачи по-новому часто проливает свет на её подлинное содержание и указывает прямой путь к выбору прямых решений.

Если решение некоторой задачи сводится даже к системе линейных алгебраических уравнение, то известная теория построена в предположении, что все коэффициенты, включая и правые части, заданы точно. Такое предположение естественно для классической математики, когда система моделирует связи между реальными величинами, то её коэффициенты имеют конкретный смысл. Они часто получаются в результате измерений (прямых или косвенных) и поэтому известны приближенно. Но тогда приходится решать систему, в которой известные величины заданы приближенно.

Не так уж и редко в таких случаях малые погрешности в исходных данных вызывают достаточно большие погрешности в решениях, которые таким образом оказываются практически непригодными, неустойчивыми, а соответствующие им задачи плохо обусловленными.

Конечно, при рассмотрении прикладных задач важно знать, какое решение найдено: неустойчивое или устойчивое, добротное, которое может быть использовано на практике. Ответ на этот вопрос можно получить на основе применения ЭВМ.

1) 2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОСНОВНЫХ ЛОГИЧЕСКИХ СВЯЗОК

Логические связки служат для образования сложных высказываний из простых. Понятие «высказывание» в логике является первичным, оно не определяется, а поясняется. Под высказыванием понимается повествовательное предложение, о котором можно сказать, разумно считать, что оно либо истинно, либо ложно. Какие-либо другие смысловые характеристики высказываний игнорируются. 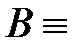Высказывания будем обозначать большими латинскими буквами А, В, С … Например, А {2 – четное число}, {6 – нечетное число}, 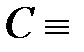{пять больше семи}, 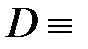{Земля – планета солнечной системы}, 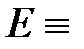{Луна – искусственный спутник Земли}.

Сразу видно, какие из приведенных высказываний являются истинными (И) и, какие – ложными (Л). Будем также обозначать истинное высказывание 1, ложное 0, тогда каждое высказывание будет характеризоваться цифрами 1 и 0, которые являются мерами истинности высказывания. Если имеется несколько высказываний, то из них с помощью логических связок и отрицаний можно построить новые высказывания.

Из каждого высказывания А можно построить его отрицание, т.е. высказывание «неверно, что имеет место А» или, короче «не А», что обозначается как «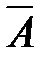». Итак, отрицанием высказывания А называется новое высказывание, обозначаемое символом 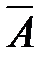, которое истинно тогда и только тогда, когда А ложно. Отрицание 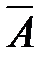высказывания задается талицей

А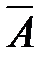

Отсюда видно, что, каково бы ни было А из двух высказываний А, 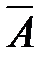одно является истинным, а другое ложным.

Дата добавления: 2015-04-24