Третья теория прочности. В третьей теории прочности критерием принимается наибольшее касательное напряжение

В третьей теории прочности критерием принимается наибольшее касательное напряжение. Согласно этой теории опасное состояние наступает, если наибольшие касательные напряжения достигают опасного значения.

Условие прочности имеет вид:

,

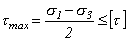где .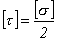

Откуда

5. Диаграмма растяжения образца из малоуглеродистой стали

ДИАГРАММОЙ РАСТЯЖЕНИЯ называется график, показывающий функциональную зависимость между нагрузкой и деформацией при стати­ческом растяжении образца до его разрыва

На диаграмме растяжения OABCDEG показаны 7 характерных точек, соответствующих определённому уровню нагрузки и ограничивающих 6 различных зон деформирования:

OA – зона пропорциональности (линейной упругости);

AB – зона нелинейной упругости;

BC – зона упругопластических деформаций;

CD – зона текучести (пластических деформаций);

DE – зона упрочнения;

EG – зона закритических деформаций.

6. Изгиб. Деформации при плоско поперечном изгибе прямых брусьев. Их определение. Типы балок и опор.

7. Кручение. Деформации при кручении бруса с круглого поперечного сечения.

Кручение – понимается такой вид нагружения при котором в поперечных сечениях бруса возникает только крутящий момент.

Опыты показывают, что если на поверхности бруса круглого сечения нанести прямоугольную сетку, а на торцевой поверхности нанести радиальные линии (рис.5.5), то после деформации кручение окажется что:

- все образующие поворачиваются на один и тот же угол, а прямоугольники, нанесенные на поверхности, превращаются в параллелограммы;

- торцевые сечения остаются круглыми, плоскими, расстояния между ними не меняются;

- каждое сечение поворачивается относительно другого на некоторый угол, называемый углом закручивания;

- радиальные линии на торцевой поверхности остаются прямыми.

Деформация кручения вызывается скручивающими моментами, плоскости действия которых перпендикулярны продольной оси (рис. 6.2).При кручении возникает один внутренний силовой фактор - крутящий момент Mk.

1. После приложения скручивающего момента наблюдаем следующее: образующие цилиндра превращаются в линии одинакового наклона к оси стержня; параллельные круги не искривляются и расстояние между ними остается неизменным, радиусы, проведенные в торцевых сечениях, остаются прямыми (рис. 6.3). Таким образом, при построении теории напряженно-деформированного состояния вала при кручении пользуются следующими гипотезами: Поперечные сечения вала остаются при деформации плоскими и перпендикулярными к оси вала. Они лишь поворачиваются одно относительно другого на некоторый угол закручивания, обозначаемый φ. (гипотеза плоских сечений).
2. Расстояния между поперечными сечениями остаются неизменными.
3. Радиусы, проведенные в поперечных сечениях, при деформации не искривляются. Рассмотрим некоторый участок вала длиной dz, выделенный из вала (рис. 6.4). Пусть угол поворота сечения m-m относительно неподвижного будет φ,тогда угол поворота сечения n-n, расположенного на расстоянии z, будет φ + dφ. Следовательно, угол закручивания участка вала длиной dz равен dφ.

8. Плоский поперечный изгиб. Основные определения. Типы балок и опор

Если в поперечных сечениях бруса кроме изгибающего момента действует так же поперечная сила – изгиб называется поперечным. Втаком случае в поперечных сечениях возникает не только нормальное но и касательное напряжение.

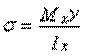Так как касательные напряжения в общем случае распределены по сечению неравномерно, то при поперечном изгибе поперечные сечения балки, строго говоря, не остаются плоскими. Однако при 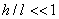(где h - высота поперечного сечения, l - длина балки) ока­зывается, что эти искажения заметным образом не сказываются на работе балки на изгиб. В данном случае гипотеза плос­ких сечений и в случае чистого изгиба с достаточной точно­стью приемлема. Поэтому для расчета нормальных напряже­ний 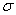применяют ту же формулу (5

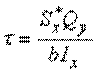. Полученная формула носит имя русского ученого Д.И. Журавского.

Условие прочности по касательным напряжениям:

,

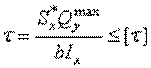Основные типы балок и опор;
Балка-это брус работающий на изгиб.
1)Консоль

2) Двух опорная балка

Пролет- это расстояние между опорами
3)Двухопорная балка с консолью.
4) Многопролетная балка; 3-ех пролетная с консолью

5) Двухопорная балка с консолью и врезанным шарниром
Два внутренних силовых фактора возникающие при прямом изгибе в поперечном сечении
1) поперечная сила Q
2) изгибающий момент М

9. Перемещения, деформации, напряжения.

Под действием внешних сил твердые тела изменяют свою гео­метрическую форму, то есть деформируются. Если в теоретической механике тела считаются абсолютно жесткими, то в сопротивлении материалов тела обладают способностью деформироваться, т.е. под действием внешней нагрузки изменять свои начальные размеры и форму. Точки тела при этом неодинаково перемещаются в пространстве. Вектор 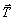, имеющий свое начало в точке А недефор­мированного состояния, а конец в т. деформированного состоя­ния, называется вектором полного перемещения т. А (рис. 1.8, а). Его проекции на оси xyz называются осевыми перемещениями и обозначаются u, v и w, соответственно.

Для того, чтобы охарактеризовать интенсивность изменения формы и размеров тела, рассмотрим точки А и В его недеформиро­ванного состояния, расположенные на расстоянии 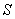друг от друга (рис. 1.8, б).

Рис. 1.8

Пусть в результате изменения формы тела эти точки перемес­тились в положение и 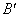, соответственно, а расстояние между ними увеличилось на величину D S и составило S + D S. Величина

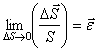(1.9)

называется линейной деформацией в точке А по направлению АВ. Если рассматривать деформации по направлениям координатных осей , то в обозначения соответствующих проекций линейной деформации вводятся индексы , , .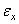

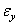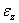Линейные деформации 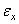, , 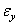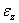характеризуют изменения объема тела в процессе деформирования, а формоизменения тела - угловыми деформациями. Для их определения рассмотрим прямой угол, образованный в недеформированном состоянии двумя отрез­ками ОD и ОС (рис. 1.8, б). При действии внешних сил указанный угол DOC изменится и примет новое значение 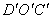. Величина

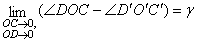(1.10)

называется угловой деформацией, или сдвигом в точке О в плос­кости СОD. Относительно координатных осей деформации сдвига обозначаются , , .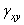

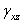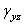Совокупность линейных и угловых деформаций по различным направлениям и плоскостям в данной точке образует деформиро­ванное состояние в точке.

Дата добавления: 2015-04-24