Третья теория прочности

Вторая теория прочности

Во второй теории прочности за критерий принимается наибольшая деформация. Согласно этой теории опасное состояние материала наступает тогда, когда линейные деформации достигают некоторого опасного значения. Для пластичного материала условие прочности имеет вид

,

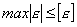где .

Если, например ,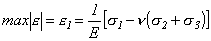

то .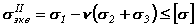

Для хрупкого материала условие прочности имеет вид

,

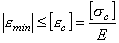
Первая теория дает удовлетворительное совпадение с опытными данными только для хрупких материалов. Вторая практически в настоящее время не применяется.

В третьей теории прочности критерием принимается наибольшее касательное напряжение. Согласно этой теории опасное состояние наступает, если наибольшие касательные напряжения достигают опасного значения.

Условие прочности имеет вид:

,

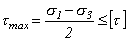где .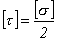

Откуда

33.Вывод формулы касательных напряжений при плоском поперечном изгибе.

(в тетради)

34.Общие принципы расчета конструкций.

В результате расчета нужно получить ответ на вопрос, удовлет­воряет или нет конструкция тем требованиям прочности и жест­кости, которые к ней предъявляются. Для этого необходимо прежде всего сформулировать те принципы, которые должны быть положе­ны в основу оценки условий достаточной прочности и жесткости.

Методы расчета конструкций выбираются в зависимости от условий работы конструкций и требований, которые к ней предъ­являются. Так, наиболее распространенным методом расчета деталей машин на прочность является расчет по допускаемым на­пряжениям. В основу этого метода положено предположение, что определяющим параметром надежности конструкции является напряжение или, точнее говоря, напряженное состояние в точке. Расчет выполняется в следующем порядке.

На основании анализа напряженного состояния конструкции выявляется та точка сооружения, где возникают наибольшие расчетные (рабочие) на­пряжения . Расчетная величина напряжений сопоставляется с пре­дельно допустимой величиной напряжений для данного материала, полученной на основе предварительных лабораторных испытаний. Чтобы не нарушилась прочность элемента, рабочие напряжения в любой его точке должны быть меньше предельных. Для особо ответственных конструкций, для которых требуется не допускать возникновения пластических деформаций, за величину принимается . В тех случаях, когда допустимо возникновение пластических деформаций, как правило, принимается 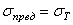. Для хрупких материалов, а в неко­торых случаях и умеренно пластических материалов, принимается .

Для надежной работы элемента нельзя допустить, чтобы рабочие (расчетные) напряжения в наиболее напряженной точке были близки к предельным, нужно обеспечить запас прочности.

Отношение предельного напряжения для материала, из которого изготовлен элемент конструкции, к максимальному рабочему напряжению называют коэффициентом запаса прочности

. (1.14)

Выбор коэффициента запаса прочности – один из основных и наиболее ответственных этапов расчета на прочность. При заниженном коэффициенте запаса прочности снижается надежность работы детали, повышается опасность ее разрушения при эксплуатации. При завышении запаса прочности увеличивается масса и стоимость детали.

Коэффициент запаса учитывает следующие основные факторы.

1. Погрешности в создании рабочей модели.

2. Возможные превышения, нагрузки в процессе эксплуатации.

3. Степень ответственности изделия.

4. Несовершенства в определении свойств материала.

5. Вероятность возможных экстремальных ситуаций (землетрясение, случайный удар и т.п.).

При назначении коэффициента запаса прочности учитывают, насколько точно можно для проектируемой детали определить рабочее и предельное напряжения. Рабочие напряжения нельзя определить абсолютно точно, так как фактические, действующие на элемент конструкции нагрузки могут существенно отличаться от используемых в расчете. В процессе эксплуатации конструкции возможно кратковременное увеличение нагрузок (перегрузки), часто нагрузки непрерывно изменяются или носят случайный характер (например, нагрузки на крыло летящего самолета). Формулы сопротивления материалов основаны на определенных допущениях, упрощающих расчеты, и, следовательно, не обеспечивают высокой точности. В деталях сложной формы напряжения, как правило, можно определить только приближенно. Предельные напряжения, характеризующие прочность материала, также нельзя определить абсолютно точно вследствие непостоянства химического состава сплавов в различных плавках, отклонений в режимах технологического процесса изготовления материалов, погрешностей при испытании образцов. При расчете элемента конструкции необходимо учитывать возможные последствия его разрушения.

Так как все факторы, влияющие на прочность элемента конструкции, учесть точно в расчете невозможно, в расчет вводят требуемый (допускаемый) коэффициент запаса прочности , гарантирующий надежную работу элемента конструкции в течение требуемого срока службы (табл.1.2)

Таблица 1.2. Ориентировочные значения допускаемого коэффициента

запаса прочности

Вид материала	Характер нагрузки	Коэффициент запаса прочности
Пластичный	Статическая	2,4-2,6
Ударная	2,8-5,0
Повторно-переменная	5,0-15,0
Хрупкий	Статическая	3,0-9,0

Часто этот коэффициент представляют в виде произведения частных коэффициентов запаса , каждый из которых учитывает влияние на прочность элемента конструкции какого-либо одного ил нескольких факторов.

В каждой отрасли машиностроения существуют нормы на допускаемые запасы прочности, основанные на большом опыте расчета деталей и их эксплуатации. Определяемые по нормам коэффициенты запасы прочности называют нормативными.

Прочность элемента конструкции считают обеспеченной, если расчетный коэффициент запаса не меньше допускаемого

. (1.15)

Это равенство называют условием прочности.

Если установлен допускаемый коэффициент запаса прочности и для выбранного материала известно предельное напряжение, определяют максимальное напряжение, которое можно допустить для надежной работы элемента конструкции. Такое напряжение называют допускаемым

. (1.16)

Часто величина допускаемого напряжения берется из таблиц, составленных на основе действующих норм (см. «Справочные данные»).

В практических расчетах считают, что прочность элемента конструкции обеспечена, если возникающие в нем максимальные напряжения не превышают допускаемых. Условие прочности имеет вид

. (1.17)

Если материал имеет различные предельные напряжения при растяжении и сжатии, то допускаемое напряжение обозначают соответственно 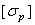и .

Чтобы уточнить, какое напряжение принято в качестве предельного (предел текучести или прочности ), иногда в обозначения расчетных и допускаемых коэффициентов запаса прочности вводят соответствующие индексы: ; ; ; .

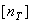Указанный метод является не единственным. Например, на практике в некоторых случаях используется метод расчета конст­рукций по разрушающим нагрузкам. В этом методе путем расчета определяется предельная нагрузка, которую может выдержать кон­струкция, не разрушаясь и не изменяя существенно свою форму. Предельная (разрушающая) нагрузка сопоставляется с проектной нагрузкой, и на этом основании делается вывод о несущей способ­ности конструкции в эксплуатационных условиях.

Условие прочности можно представить в виде

, (1.18)

где - коэффициент запаса прочности, принимаемый таким же, как и в методе допускаемых напряжений.

При определении разрушающей нагрузки для конструкций из пластичного материала применяется схематизированная диаграмма напряжений - диаграмма Прандтля (рис.1.9). Схематиза­ция диаграммы заключается в предположении, что материал на на­чальном этапе деформирования находится в упругой стадии вплоть до предела текучести, а затем материал обладает неограниченной площадкой текучести. Материал, работающий по такой диаграмме, называется идеально упруго-пластическим. Такая схема­тизированная диаграмма деформирования в большей степени соот­ветствует действительной диаграмме деформирования материала, имеющего ярко выраженную площадку текучести, т.е. пластичным материалам.

Следует заметить, что определение разрушающей нагрузки возможно только для несложных расчетных схем.

Рис.1.9

Если необходимо добиться наименьших изменений фор­мы конструкции, то производится расчет по допускаемым пе­ремещениям. Это не исключает и одновременной проверки сис­темы на прочность по напряжениям.

В случае расчета конструкции по допускаемым перемещениям необходимо удов­летворять условию

, (1.19)

где и 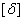- максимальное и допускаемое значения переме­щения.

Для расчета строительных конструкций применяется метод расчета по предельным состояниям.

Данный метод предполагает обеспечить такие условия работы конструкции, при которых исключалась бы возможность наступления расчетного предельного состояния, под которым понимают потерю способности сопротивляться внешним силовым воздействиям или отвечать заданным эксплуатационным требованиям.

34.Удлинение стержня и закон Гука

(в тетради)

35. Внешние и внутренние силы. Метод сечений.

Силы являются мерилом механического взаимодействия тел. Если конструкция рассматривается изолированно от окружающих тел, то действие последних на нее заменяется силами, которые на­зываются внешними. Внешние силы, действующие на тело, мож­но разделить на активные (независимые) и реактивные. Реак­тивные усилия возникают в связях, наложенных на тело, и опреде­ляются действующими на тело активными усилиями.

По способу приложения внешние силы делятся на объемные и поверхностные.

Объемные силы распределены по всему объему рассматривае­мого тела и приложены к каждой его частице. В частности, к объ­емным силам относятся собственный вес сооружения, магнитное притяжение или силы инерции. Единицей измерения объемных сил является сила, отнесенная к единице объема - кН/м³.

Поверхностные силы приложены к участкам поверхности и являются результатом непосредственного контактного взаимодействия рас­сматриваемого объекта с окружающими телами. В зависимости от соотношения площади приложения нагрузки и общей площади поверхности рассматриваемого тела, поверхностные нагрузки под­разделяются на сосредоточенные и распределенные. К первым от­носятся нагрузки, реальная площадь приложения которых несоиз­меримо меньше полной площади поверхности тела (например, воз­действие колонн на фундаментную плиту достаточно больших раз­меров можно рассматривать как действие на нее сосредоточенных усилий). Если же площадь приложения нагрузки сопоставима с площадью поверхности тела, то такая нагрузка рассматривается как распределенная. Примером может служить собственный вес балки, действие снеговой или ветровой нагрузки на сооружение, давление жидкости в резервуаре. Распределенная нагрузка может действовать и по линии как, например, при соприкасании двух цилиндров при параллельном расположении их осей. Сосредоточенные усилия измеряются в кН, а распределенные - кН/м² или кН/м.

По времени действия внешние нагрузки (силы) разделяются на постоянные и временные. Собственный вес зданий – это постоянно действующая нагрузка; поезд, идущий через мост, - это нагрузка временная.

По характеру изменения силы во времени различают нагрузки статические и динамические. Статические нагрузки (постоянные) - такие, которые изменяют свою величину или точку приложения (направление) с очень небольшой скоростью, так что возникающими при этом ускорениями (силами инерции) можно пренебречь. Динамические нагрузки - изменяются во времени с большой скоростью, при этом силы инерции должны быть учтены, так как оказывают существенное влияние на конструкцию. Динамические нагрузки подразделяются на внезапно приложенные, повторно-переменные и ударные. Примером внезапно приложенной нагрузки может служить действие веса железнодорожного состава, проходящего через мост; повторно-переменной – нагрузка на шатун в двигателе внутреннего сгорания; ударной – действие силы удара молота на его фундамент или гидравлический удар в гидросистеме. Ударные нагрузки возникают также в случае плохой пригонки или износа сопряженных деталей, когда зазоры превышают величину, допустимую по конструктивным и технологическим условиям. Например, при износе зубьев шестерен или деталей шариковых подшипников в машине возникают характерные стуки, свидетельствующие о возникновении ударных нагрузок, быстро приводящих к выходу конструкции из строя.

Скорость роста усилий при динамическом нагружении не обеспечивает равновесности процессов, протекающих в материале, в результате чего возникают многочисленные нарушения внутренней структуры материала. При систематическом чередовании нагружения и разгрузки накопление дефектов структуры ведет к возникновению микроскопических трещин, слияние которых приводит к усталостному разрушению.

Взаимодействие между частями рассматриваемого тела характе­ризуется внутренними силами, которые возникают внутри тела под действием внешних нагрузок и определяются силами межмоле­кулярного воздействия. Эти силы сопротивляются стремлению внешних сил разрушить элемент конструкции, изменить его форму, отделить одну часть от другой.

В брусе сечение проводят перпендикулярно его оси. Такое сечение называют поперечным.

Величины внутренних усилий определяются с применением метода сечений, суть которого заключается в следующем. Если при действии внешних сил тело находится в состоянии равновесия, то любая отсеченная часть тела вместе с приходящимися на нее внешними и внутренними усилиями также находится в равновесии, следовательно, к ней применимы уравнения равновесия.

Рассмотрим тело, имеющее форму бруса (рис. 1.4, а).

Пусть к нему приложена некоторая система внешних сил Р ₁, Р ₂, Р ₃,..., Р_n, удовлетворяющая условиям равновесия, т.е. при дейст­вии указанных внешних сил тело находится в состоянии равнове­сия.

Если рассечь брус сечением А на две части и правую отбросить, то, т.к. связи между частями тела устранены, необходимо действие правой (отброшенной) части на левую заменить некоей системой внутренних сил (P_А ), действующей в сечении А (рис. 1.4, б).

Рис. 1.4

Обозначая через 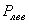и 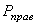суммы внешних сил, приложен­ных соответственно, к левой и правой частям бруса (относительно сечения А), и учитывая, что

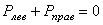(1.1)

для отсеченных частей бруса получим следующие очевидные соот­ношения:

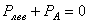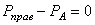; . (1.2)

Последние соотношения показывают, что равнодействующая внутренних сил Р_А в сечении А может определяться с равным успе­хом из условий равновесия либо левой, либо правой частей рассе­ченного тела. В этом суть метода сечений.

Внутренние усилия должны быть так распределены по сече­нию, чтобы деформированные поверхности сечения А при совме­щении правой и левой частей тела в точности совпадали. Это тре­бование в механике твердого деформируемого тела носит название условия неразрывности деформаций.

Воспользуемся правилами статики и приведем систему внут­ренних сил 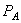к центру тяжести сечения А в соответствии с прави­лами теоретической механики. В результате получим главный век­тор сил 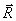и главный вектор момента 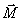(рис. 1.5). Далее выбира­ем декартову систему координат xyz с началом координат, совпада­ющим с центром тяжести сечения А. Ось направим по нормали к сечению, а ос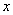и и 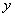расположим в плоскости сечения. Спроекти­ровав главный вектор сил 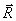и главный момент 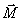на координат­ные оси x, y, z, получаем шесть составляющих: три силы N_z, Q_x, Q_y и три момента M_z, M_x, M_y, называемых внутренними силовы­ми факторами в сечении бруса.

Составляющая N_z называется нормальной, или продольной си­лой в сечении. Силы Q_x и Q_y называются поперечными усилиями. Момент M_z называется крутящим моментом, а моменты M_x и M_y - изгибающими моментами относительно осей x и y, соответственно.

При известных внешних силах все шесть внутренних силовых факторов в сечении определяются из шести уравнений равновесия, которые могут быть составлены для отсеченной части.

Пусть R^*, M^* - результирующая сила и результирующий момент, действующие на отсеченной части тела. Если тело при действии полной системы внешних сил находится в равновесном состоянии, то условия равновесия отсеченной части тела имеет вид:

(1.3)

Последние два векторные уравнения равновесия дают шесть скалярных уравнений в проекциях на декартовых осях координат:

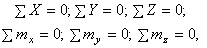(1.4)

которые, в общем случае составляют замкнутую систему алгебраических уравнений относительно шести неизвестных внутренних усилий: , , , , , .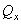

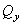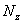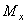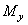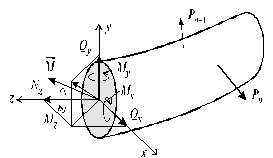
Рис. 1.5

Следовательно, если полная система внешних сил известна, то по методу сечений, всегда можно определить все внутренние усилия действующих в произвольно взятом сечении тела. Данное положение является основополагающим обстоятельством в механике твердого деформируемого тела.

В общем случае в сечении могут иметь место все шесть силовых факторов. Однако достаточно часто на практике встречаются случаи, когда некоторые внутренние усилия отсутствуют - такие виды нагружения бруса получилиспециальные названия (табл.1.1).

Таблица 1.1. Простейшие случаи сопротивления

Вид напряженного состояния	Nz	Qx	Qy	Mz	Mx	My
Растяжение/сжатие	+
Кручение				+
Чистый изгиб относительно оси х					+
Чистый изгиб относительно оси у						+
Поперечный изгиб относительно оси х			+		+
Поперечный изгиб относительно оси у		+				+

Примечание: + означает наличие усилия, 0 - его отсутствие.

Сопротивления, при которых в поперечном сечении бруса дей­ствует одно внутреннее усилие, условно называются простыми. При одновременном действии в сечении бруса двух и более усилий (например, изгиб с кручением) сопротивление бруса называется сложным.

В заключение заметим, что при выполнении практических рас­четов, для наглядности, как правило, определяются графики функ­ций внутренних силовых факторов относительно координатной оси, направленной вдоль продольной оси стержня. Графики изме­нения внутренних усилий вдоль продольной оси стержня называ­ются эпюрами.

Дата добавления: 2015-04-24