Непрерывная на отрезке функция принимает свои наименьшее и наибольшее значения на этом отрезке

Следствие. Пусть функция непрерывна на отрезке . Тогда для любого числа 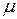, удовлетворяющего неравенствам , существует точка такая, что .

$ По доказанной теореме, существуют такие точки , принадлежащие отрезку , что . Рассмотрим отрезок числовой оси, соединяющий эти точки. Пусть, для определённости, . Тогда функция непрерывна на отрезке . По следствию теоремы 16.1, для любого 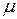, удовлетворяющего неравенствам, существует точка такая, что .#

Замечание. Доказанные утверждения означают, что непрерывная на отрезке функция принимает на нём все свои значения, от наименьшего до наибольшего. Разумеется, таким свойством могут обладать не только непрерывные функции. Например, функция принимает все значения от -1 до +1, однако имеет разрыв в точке .

Отметим ещё одно важное следствие теоремы 17.2.

Дата добавления: 2015-04-24