
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Типовой пример 1 страница
|
|
|
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Важным направлением развития межрегиональных сопоставлений выступает построение интегральных показателей уровня жизни населения. Программой развития ООН разработан интегральный показатель – Индекс развития Человеческого Потенциала (ИРЧП). Данный показатель включает три компоненты уровня жизни: долголетие, образование, доход.
В таблице 1 представлены статистические данные (N=100), характеризующие компоненты ИРЧП по областям и краям Российской Федерации. X – материальный доход за месяц в условных единицах, Y – продолжительность жизни.
Таблица 1
Статистические данные типового примера
| N | ||||||||||||
| X | ||||||||||||
| Y |
| N | ||||||||||||
| X | ||||||||||||
| Y |
| N | ||||||||||||
| X | ||||||||||||
| Y |
| N | ||||||||||||
| X | ||||||||||||
| Y |
| N | ||||||||||||
| X | ||||||||||||
| Y |
| N | ||||||||||||
| X | ||||||||||||
| Y |
| N | ||||||||||||
| X | ||||||||||||
| Y |
| N | ||||||||||||
| X | ||||||||||||
| Y |
| N | ||||
| X | ||||
| Y |
Сравнение индексов долголетия, образованности и уровня жизни на внутрироссийском уровне даёт возможность уточнить приоритетность соответствующих в стране программ человеческого развития, а также определить желательные масштабы их финансирования на национальном и региональном уровнях. Для этого требуется провести анализ данных Таблицы 1:
1. Построить эмпирическую функцию распределения, полигон и гистограмму для случайной величины Х;
2. Построить точечные и интервальные оценки для математического ожидания и дисперсии генеральной совокупности Х;
3. Сделать статистическую проверку гипотезы о нормальном законе распределения случайной величины Х;
4. Составить корреляционную таблицу по сгруппированным данным;
5. Найти линейную корреляционную модель зависимости дохода (Х) от фактора долголетия (Y);
6. Оценить тесноту корреляционной связи;
7. Оценить степень близости модели к статистическим данным;
8. Вычислить прогнозные значения фактора Х и точность прогноза для значений фактора, равных 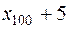 и
и 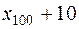 .
.
Решение.
Составим ранжированный ряд для случайной величины Х.
Таблица 2
Ранжированный ряд случайной величины Х
| N | ||||||||||||
| X | ||||||||||||
| Y |
Продолжение таблицы 2
| N | ||||||||||||
| X | ||||||||||||
| Y |
| N | ||||||||||||
| X | ||||||||||||
| Y |
| N | ||||||||||||
| X | ||||||||||||
| Y |
| N | ||||||||||||
| X | ||||||||||||
| Y |
| N | ||||||||||||
| X | ||||||||||||
| Y |
| N | ||||||||||||
| X | ||||||||||||
| Y |
| N | ||||||||||||
| X |
| N | ||||
| X | ||||
| Y |
Для удобства расчётов составим новую Таблицу 3, в которой отразим частоты появления случайных величин  и относительные частоты
и относительные частоты  .
.
Таблица 3
Дискретный вариационный ряд
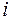
| |||||

| |||||

| |||||

| 
| 
| 
| 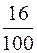
| 
|
В данном примере случайная величина Х распределена с шагом h=5.
Рассчитаем эмпирическую функцию распределения в виде «нарастающей относительной частоты» (Таблица 4).
Таблица 4
Расчёт эмпирической функции распределения
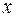
| 
|

| |
220 
| 
|
225< 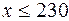
|  + + 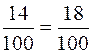
|
230< 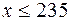
| 
|
235< 
| 
|

| 
|
Построим эмпирическую функцию распределения рис.1







Рис.1
Экспериментальные данные, представленные в виде вариационного ряда можно представить графически в виде ломаной линии (полигона), связывающей на плоскости точки с координатами ( ), где
), где  - относительная частота (рис. 2). На этом же рисунке отобразим пунктирной линией выравнивающие (теоретические частоты) частоты.
- относительная частота (рис. 2). На этом же рисунке отобразим пунктирной линией выравнивающие (теоретические частоты) частоты.
 |
Рис.2
Предположим, что случайная величина Х распределена нормально, тогда выравнивающие частоты могут быть найдены по формуле:
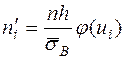 , (57)
, (57)
где n – число испытаний,
h – длина частичного интервала,
 - выборочное среднее квадратическое отклонение,
- выборочное среднее квадратическое отклонение,
 (
(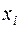 - середина
- середина 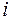 -го частичного интервала),
-го частичного интервала),
 . (58)
. (58)
Результаты вычислений отобразим в Таблице 5.
Таблица 5
Расчёт выравнивающих частот
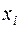
| 
| 
| 
| 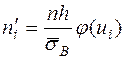
| 
| 
|
| -11,7 -6,7 -1,7 3,3 8,3 | -2,18 -1,25 -0,32 0,62 1,55 | 0,04 0,18 0,38 0,33 0,12 | 3,74 16,82 35,51 30,84 11,22 | 0,04 0,17 0,36 0,31 0,12 |
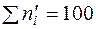
Сравнение графиков наглядно показывает близость выравнивающих частот к наблюдаемым и подтверждает правильность допущения о том, что обследуемый признак распределён нормально.
2) Найдём числовые характеристики вариационного ряда, используя Таблицу 3.
Средняя арифметическая (9):


Средняя гармоническая (10):

Средняя квадратическая (11):

Средняя геометрическая (12):

Сделаем проверку по формуле (13):

Выборочная дисперсия (14):

Среднее квадратическое отклонение (15):

Выборочная мода: 
Выборочная медиана: 
Коэффициент вариации (16):
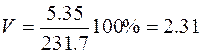
Размах варьирования (17):
R=240-220=20
Среднее абсолютное отклонение (18):

«Исправленные» дисперсия и среднеквадратическое отклонение (19):
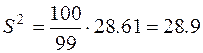 ,
, 
 .
.
Доверительный интервал для оценки математического ожидания с надёжностью 0,95 найдём по формуле (21). Из соотношения  находим значение функции Лапласа:
находим значение функции Лапласа: 
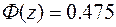 . По таблице значений функции Лапласа (Приложение 4) находим z=1,96. Таким образом,
. По таблице значений функции Лапласа (Приложение 4) находим z=1,96. Таким образом,

230,65<a<232,75
Доверительный интервал для оценки среднего квадратического отклонения случайной величины находим по формуле (22). На основании данных значений  и n=100 по таблице (Приложение 5) находим значение q=0,143. Таким образом,
и n=100 по таблице (Приложение 5) находим значение q=0,143. Таким образом,
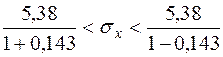
4,71< 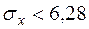
Моменты k-го порядка (23):


Асимметрия (24):

Оценка степени существенности (25):

отношение  <3, значит асимметрия не существенна.
<3, значит асимметрия не существенна.
Эксцесс (26):

3)Проведём статистическую проверку гипотезы о нормальном распределении. Нормальный закон распределения имеет два параметра (r=2): математическое ожидание и среднее квадратическое отклонение.
Для расчёта теоретических частот  воспользуемся табличными значениями функции Лапласа
воспользуемся табличными значениями функции Лапласа  Алгоритм вычисления
Алгоритм вычисления  состоит в следующем:
состоит в следующем:
- по нормированным значениям случайной величины Z находим значения  , а затем
, а затем  :
:

 =0,5+
=0,5+  .
.
Например,
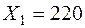 ;
;  ;
; 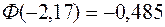 ;
;
 ;
;
- находим  ;
;
- находим  и если некоторое
и если некоторое  то соответствующие группы объединяются с соседними.
то соответствующие группы объединяются с соседними.
Результаты вычисления 
 и
и  приведены в таблице №6.
приведены в таблице №6.
По формуле
 (59)
(59)
можно сделать проверку расчётов.


По таблице Приложения 6 находим  по схеме: для уровня значимости
по схеме: для уровня значимости  0,05 и числа степеней свободы
0,05 и числа степеней свободы 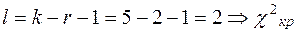 =6,0. Следовательно, критическая область – (6;
=6,0. Следовательно, критическая область – (6;  ). Величина
). Величина  =44,21 входит в критическую область, поэтому гипотеза о том, что случайная величина Х подчинена нормальному закону распределения отвергается.
=44,21 входит в критическую область, поэтому гипотеза о том, что случайная величина Х подчинена нормальному закону распределения отвергается.
При 
 =4,61. Критическая область – (4,61;
=4,61. Критическая область – (4,61;  ). Величина
). Величина  =44,21 также входит в критическую область и гипотеза о нормальном законе распределения величины Х отвергается.
=44,21 также входит в критическую область и гипотеза о нормальном законе распределения величины Х отвергается.
При 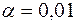
 =9,2. Критическая область – (9,2;
=9,2. Критическая область – (9,2;  ).
).
Величина  =44,21 также входит в критическую область и гипотеза о нормальном законе распределения величины Х отвергается.
=44,21 также входит в критическую область и гипотеза о нормальном законе распределения величины Х отвергается.
Таблица 6
Определение 
| i | 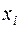
| 
| 
| 
| 
| 
| 
| 
|
| -0,485 | 0,015 | 0,106 | 0,091 | 9,1 | 2,86 | |||
| -0,394 | 0,106 | 0,375 | 0,269 | 26,9 | 6,17 | |||
| -0,126 | 0,375 | 0,729 | 0,355 | 35,5 | 3,13 | |||
| 0,229 | 0,729 | 0,938 | 0,209 | 20,9 | 1,15 | |||
| 0,438 | 0,938 | 1,0 | 0,062 | 6,2 | 30,9 |

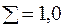

Данные Таблицы 2 сгруппируем в корреляционную Таблицу 7.
Таблица 7
Корреляционная таблица
| Y\X | 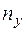
| |||||
| - | - | - | ||||
| - | - | - | ||||
| - | - | |||||
| - | - | |||||
| - | - | - | ||||

| 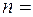 100 100
|
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 366; Нарушение авторских прав?; Мы поможем в написании вашей работы!