Применение основной задачи линейного программирования к решению некоторых экономических задач

Двойственная задача линейного программирования.

В 2.2.2 мы рассматривали общую задачу линейного программирования. Рассмотрим теперь другую экономическую задачу на том же предприятии с теми же исходными данными.

Необходимо определить такие цены

(y ₁ ³ 0, y ₂ ³ 0,…, y_m ³ 0) (2.2.6)

всех ресурсов, чтобы сумма потраченных средств на их приобретение была бы минимальна, т.е.

Z = b ₁ y ₁ + b ₂ y ₂ +…+ b_m y_m à min. (2.2.7)

С другой стороны, предприятию будет выгодно продать ресурсы в случае, если выручка от их продажи будет не менее той суммы, которую предприятие может получить при изготовлении продукции из этих ресурсов. Т.к., на производство единицы продукции j расходуется a _{1 j} единиц ресурса 1, a _{2 j} единиц ресурса 2,…, a_mj единиц ресурса m, то для обеспечения выгодности продажи ресурсов необходимо выполнение следующих неравенств:

a ₁₁ y ₁ + a ₂₁ y ₂ +…+ a_{m 1} y_m ³ с ₁,

a ₁₂ y ₁ + a ₂₂ y ₂ +…+ a_{m 2} y_m ³ с ₂,

…………………………………. (2.2.8)

a _{1 n} y ₁ + a _{2 n} y ₂ +…+ a_mn y_m ³ с_n,

Полученная экономико-математическая модель называется двойственной или сопряженной по отношению к исходной.

Цены ресурсов y ₁, y ₂,…, y_m получили различные названия: учетные, неявные, теневые. В отличие от «внешних» цен с ₁, с ₂,…, с_n на продукцию, известных, как правило, до начала производства, цены ресурсов y ₁, y ₂,…, y_m являются внутренними, ибо они определяются непосредственно в результате решения задачи, поэтому их чаще называют объективно обусловленными оценками ресурсов (Л.В.Канторович).

Построим двойственную задачу для примера 2.2.1:

Z = 12 y ₁ + 18 y ₂ +15 y ₃ à min. (2.2.9)

2 y ₁ + 2 y ₂ + y ₃ ³ 5,

y ₁ + 3 y ₂ + 3 y ₃ ³ 6, (2.2.10)

y ₁ ³ 0, y ₂ ³ 0, y 3 ³ 0.

Из алгебраических соображений легко показать, что F £ Z, откуда max F =min Z, если они существуют (основная теорема двойственности).

В нашем примере 2.2.1 max F = min Z = 40.5, и объективно обусловленные оценки y ₁= 0.75, y ₂ = 1.75, y ₃ = 0, вычисленные простым счетом в 2.2.5, являются решением двойственной задачи (2.2.9) - (2.2.10).

Действительно, 12´0.75 + 18´1.75 + 15´0 = 40.5.

Из выражения (2.2.9) видно, что если увеличить в условии задачи какое-либо ресурсное ограничение b _i на единицу, то Z (и следовательно F) также увеличится ровно на y_i.

Однако прямая и двойственная ей задача линейного программирования имеют и экономическое истолкование. Так, в задачах на распределение ограниченных ресурсов в производстве оптимальный план можно получить, либо минимизируя издержки для заданной программы, либо максимизируя выпуск при заданной общей сумме издержек. Двойственными аспектами одной и той же задачи являются распределение ресурсов и оценка их. Если для ресурсов не существует рыночных цен, то необходимо их создать, ввести систему условных или расчетных цен.

Рассмотрим теперь пример 2.2.2 и построим для него двойственную задачу. Напомним, что в этом примере из сена и концентратов необходимо составить суточный рацион питания, калорийность которого 20 кормовых единиц, содержание белка 2000 гр., а кальция 100 грамм. Цена сена 1.5, а концентратов 2.5 усл.единиц за 1 кг. Пусть y ₁, y ₂, y ₃ - наша оценка (за единицу) полезности каждого из этих показателей. Тогда общая (условная) оценка рациона питания:

Z = 20 y ₁ + 2000 y ₂ +100 y ₃.

Мы будем стремиться максимизировать Z. Если 1 кг. сена содержит 0.5 кормовых единиц, 50г белка и 10 г кальция, то оценка его питательного содержания, т.е. 0.5 y ₁ + 50 y ₂ + 10 y ₃, не может превышать его рыночной цены (1.5). Аналогично этому для концентратов оценка питательных веществ, равная y ₁ + 200 y ₂ + 2 y ₃, не может превышать 2.5. Следовательно, двойственную задачу можно сформулировать таким образом:

Найти такие оценки питательных веществ, чтобы

Z = 20 y ₁ + 2000 y ₂ +100 y ₃ à mах (2.2.11)

при условии

0.5 y ₁ + 50 y ₂ + 10 y ₃ £ 1.5,

y ₁ + 200 y ₂ + 2 y ₃ £ 2.5, (2.2.12)

y ₁ ³ 0, y ₂ ³ 0, y ₃ ³ 0.

Мы получили двойственную задачу к примеру 2.2.2, в котором требовалось найти минимальную стоимость входящих в рацион продуктов питания при заданных рыночных ценах на эти продукты и при соблюдении ограничений в отношении потребности в питательных веществах. После введения условных оценок показателей питательности возникает двойственная задача (2.2.11) – (2.2.12), где требуется максимизировать условную оценку рациона питания при соблюдении ограничений, согласно которым расходы в расчете за единицу продукта не могут превышать его заданной рыночной цены. Цель первой, прямой задачи заключается в том, чтобы закупаемые продукты были, возможно, более дешевыми, удовлетворяя вместе с тем требованиям в отношении питательной ценности, а цель сопряженной двойственной задачи – в том, чтобы при заданных рыночных ценах на продукты получить рацион наиболее высокопитательный.

Имея краткую запись общей задачи линейного программирования в виде:

F = à max

при ограничениях:

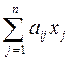£ b_i (i =1,2,…, m),

x_j ³ 0 (j =1,2,… n).

можно так же кратко записать двойственную к ней задачу:

_m

Z =å b _i y _i à min

ⁱ⁼¹

при ограничениях:

_m

å a_ijy _i ³ c _j (j =1,2,…, n),

ⁱ⁼¹

y_i ³ 0 (i =1,2,…, m).

Пример 2.2.3.Дана исходная задача:

максимизировать линейную функцию F = 2× х ₁ + 3× х ₂ ® max

при ограничениях x ₁ + 3× x ₂ £ 18,

2× x ₁ + x ₂ £ 16,

x ₂ £ 5,

3× x ₁ £ 21,

x ₁ ³ 0, x ₂ ³ 0.

Требуется составить задачу, двойственную к исходной задаче.

Решение.

Сформулируем двойственную задачу:

Z = 18× y ₁ + 16× y ₂ + 5× y ₃ + 21× y ₄ ® min

при ограничениях y ₁ + 2× y ₂ + 3× y ₄ ³ 2,

3× y ₁ + y ₂ + y ₃ ³ 3,

y _i ³ 0, i = 1, 4.

Линейное программирование возникло из практических потребностей, поэтому оно находит применение при решении широкого класса различных практических, в частности, экономических задач. Рассмотрим постановку и решение некоторых из них.

Дата добавления: 2015-04-24