Вычисление площади поверхности вращения

Вычисление длины дуги.

Для того, чтобы получить формулы для вычисления длины дуги, вспомним выведенные в 1 семестре формулы для дифференциала длины дуги.

Если дуга представляет собой график непрерывно дифференцируемой функции 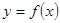, дифференциал длины дуги можно вычислить по формуле

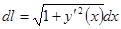. Поэтому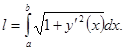

Если гладкая дуга задана параметрически 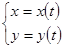, то

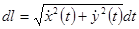. Поэтому .

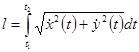Если дуга задана в полярной системе координат, то

. Поэтому .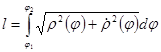

Пример. Вычислить длину дуги графика функции , . .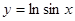

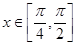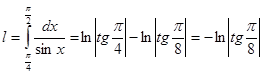Пример. Вычислить длину кардиоиды .

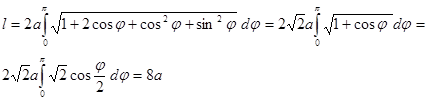
Пример. Вычислить длину одной арки циклоиды. .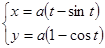

.

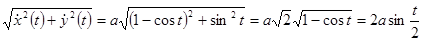
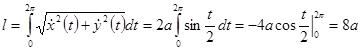Пусть гладкая дуга представляет собой график непрерывно дифференцируемой функции 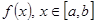. Эта дуга вращается вокруг оси OX, описывая некоторую поверхность. Требуется определить площадь этой поверхности.

Считая элемент поверхности боковой поверхностью усеченного конуса, высотой которого является отрезок 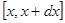, получим . Выделяя здесь линейную часть, пренебрегая квадратичным членом от дифференциала 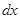, получаем 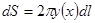. Интегрируя и применяя формулу Ньютона – Лейбница, получим

.

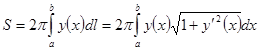Если функция задана параметрически или в полярной системе координат, то в этой формуле производится соответствующая замена переменной, формулы для дифференциала длины дуги приведены выше.

Пример. Дуга графика функции 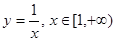вращается вокруг оси OX, образуя «ведерко». Можно ли налить в это ведерко определенное количество краски так, чтобы окрасить боковую поверхность ведерка?

Во-первых, определим, конечен ли объем ведерка.

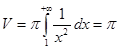, интеграл сходится, объем конечен. Ведерко будет окрашено, если будет окрашена каждая точка поверхности, т.е. в том случае, когда боковая поверхность ведерка будет конечна.

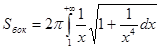. Так как 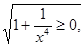а интеграл 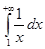расходится, то по первому признаку сравнения будет расходиться и интеграл 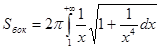. Следовательно, боковая поверхность имеет бесконечную площадь, и боковую поверхность ведерка окрасить не удастся.

Дата добавления: 2015-04-24