Лекция 14. Дифференциальные уравнения высших порядков

Уравнения первого порядка, не разрешенные относительно производной.

Рассмотрим два типа уравнений 1) .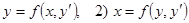

Метод введения параметра.

Обозначим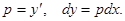

В случае 1) , .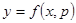

Найдем решение 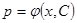, подставим в ,

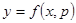получим 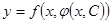- общее решение.

В случае 2)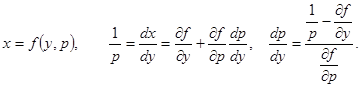

Найдем решение 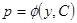, подставим в ,

получим 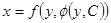- общее решение.

Уравнение Лагранжа.

Дифференцируем:

,

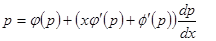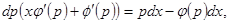
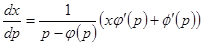- линейное уравнение.

Отыскиваем 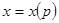и, подставляя в уравнение Лагранжа, находим .

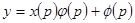Пример. 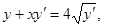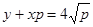- уравнение Лагранжа.

,

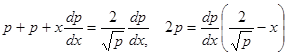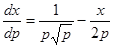- линейное уравнение по .

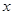Решаем его методом подстановки

.

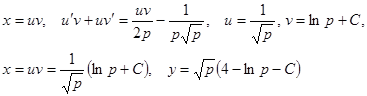Уравнение Клеро. .

Уравнение Лагранжа превращается в уравнение Клеро, если в уравнении Лагранжа положить .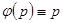

Дифференцируем обе части:

.

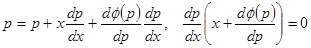1) 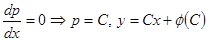- общее решение.

2) . Подставляя в уравнение, получим особое решение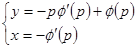

Пример.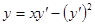

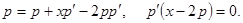
1. - общее решение

2. 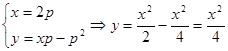- особое решение.

Дифференциальное уравнение n – ого порядка в общем виде записывается так:

.

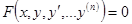Дифференциальное уравнение n – ого порядка в виде, разрешенном относительно старшей производной, выглядит так:

.

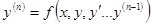Решением дифференциального уравнения n – ого порядка называется функция 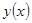, обращающая его в тождество.

Общим решением дифференциального уравнения n – ого порядка называется функция 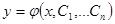такая, что

1. при любом наборе констант 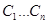эта функция является решением,

2. для любого набора начальных условий из области существования решения 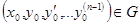найдется набор констант 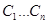, при котором функция 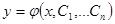удовлетворяет заданным начальным условиям, т.е. .

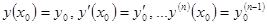Заметим, что общее решение дифференциального уравнения n – ого порядка зависит ровно от n констант.

Частным решением дифференциального уравнения n – ого порядка называется какое-либо из решений, входящих в общее решение (при конкретном выборе констант).

Общим интегралом дифференциального уравнения n – ого порядка называется функция 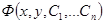, сохраняющая свои значения на решениях дифференциального уравнения.

Интегральной кривой называется график частного решения.

Общее решение представляет собой совокупность интегральных кривых.

Обычно рассматривается одна из трех задач:

1. Найти общее решение дифференциального уравнения n – ого порядка,

2. Задача Коши – найти частное решение дифференциального уравнения n – ого порядка, удовлетворяющее заданным начальным условиям,

3. Краевая задача – найти частное решение, удовлетворяющее заданным начальным условиям, одна часть которых задана в точке 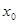, а другая часть в точке .

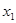Теорема Коши (существования и единственности решения задачи Коши для дифференциального уравнения n – ого порядка ).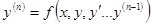

Пусть функция 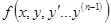и ее частные производные по переменным 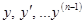определены и непрерывны в некоторой области .

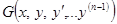Тогда для любой внутренней точки 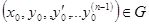существует единственное решение дифференциального уравнения, удовлетворяющее этим начальным условиям, т.е.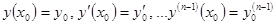

(через любую внутреннюю точку 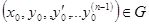проходит единственная интегральная кривая).

Пример. Рассмотрим дифференциальное уравнение второго порядка 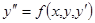. Область существования и единственности решения 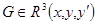заполнена непересекающимися интегральными кривыми. Через любую точку 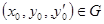проходит единственная интегральная кривая. Однако через «точку» 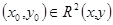проходит бесконечно много интегральных кривых, все они различаются значениями . Заметим, что в 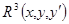«точка» 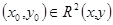представляет собой прямую .

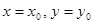Понижение порядка дифференциальных уравнений.

Мы умеем аналитически решать всего пять типов дифференциальных уравнений первого порядка: с разделяющимися переменными, однородные, линейные, Бернулли, в полных дифференциалах. Причем однородные, линейные и Бернулли тоже сводятся к уравнениям с разделяющимися переменными.

Даже решить уравнение второго порядка, не говоря уж об уравнении n-го порядка – проблема. Поэтому стараются понизить порядок дифференциального уравнения, если это возможно, чтобы свести его к известным типам уравнений первого порядка.

Если правая часть дифференциального уравнения n-го порядка зависит только от x, то интегрируя его n раз, можно получить решение.

.

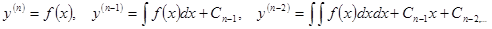
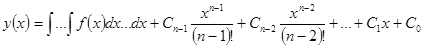Но это – очевидный случай. Рассмотрим менее очевидные случаи.

Дата добавления: 2015-04-24