Автономные системы и свойства их решений

.

Симметричная форма записи системы.

.

.

Скалярная функция 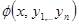является первым интегралом, если

Запишем уравнения системы в нормальной (покоординатной) форме

................................

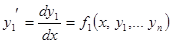
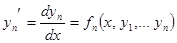
и запишем эти уравнения в симметричном виде

.

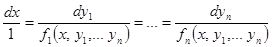Или, заменяя переменные и правые части ,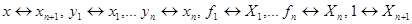

получим симметричную форму записи системы

На переходе к симметричной форме записи основан метод интегрируемых комбинаций, которым иногда удается получить один или несколько первых интегралов и понизить тем самым порядок системы или решить ее.

Пример.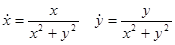

,

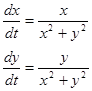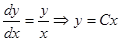
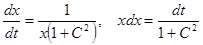
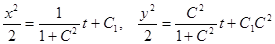
Система называется автономной, если в ее правую часть не входит явно независимая переменная: .

Решение автономной системы можно рассматривать в пространстве координат , которое принято называть фазовым пространством. Проекция интегральной кривой на это пространство называется фазовой траекторией (или просто траекторией). Вообще говоря, любую систему можно сделать автономной, вводя дополнительную фазовую координату – независимую переменную 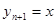и дополнительное уравнение 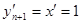. Фазовое пространство такой системы принято называть расширенным фазовым пространством.

Свойства решений автономных систем.

1) Если - решение системы, то и 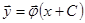тоже решение.

.

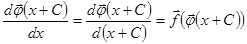Следствие. Фазовая траектория 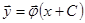- это та же фазовая траектория, что и .

В самом деле, любая точка 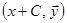первой фазовой траектории является точкой 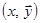второй фазовой траектории и наоборот.

2) Две фазовых траектории либо не имеют общих точек, либо совпадают.

Пусть две различных фазовых траектории 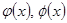имеют общую точку 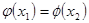. Рассмотрим решение .

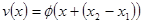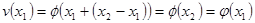. Следовательно, по теореме Коши 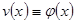. Но 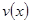- это траектория 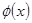, сдвинутая на по аргументу. По следствию, обе фазовые траектории являются одной фазовой траекторией.

Следствие. Множество фазовых траекторий автономной системы в фазовом пространстве представляет собой совокупность непересекающихся кривых.

Точка 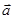называется точкой покоя (точкой равновесия) автономной системы, если .

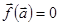3) Если точка 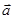- точка покоя, то 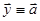- решение системы.

В самом деле, .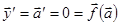

4) Любая фазовая траектория автономной системы есть траектория одного из трех типов:

1) гладкая, не самопересекающаяся кривая,

2) замкнутая гладкая кривая,

3) точка покоя.

Дата добавления: 2015-04-24