Метод вариации произвольной постоянной

Теорема о структуре общего решения неоднородной системы.

Общее решение неоднородной системы равно сумме общего решения однородной системы и частного решения неоднородной системы.

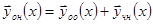
Доказательство. 1) 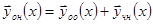- решение неоднородной системы по теореме о свойствах решений.

2) Зададим произвольные начальные условия 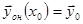. Выберем какое-либо частное решение неоднородное системы 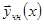и вычислим для него начальные условия в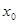 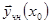. Составим систему уравнений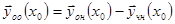 и запишем ее покоординатно.

...............................................

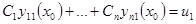
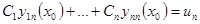
Определитель этой системы – определитель Вронского, он не равен нулю, так как составлен из линейно независимых решений, составляющих фундаментальную систему решений. Следовательно, набор констант из этой системы уравнений определяется однозначно. Теорема доказана.

Общее решение однородной системы можно записать в ви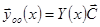де

, где - фундаментальная матрица системы, 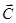- вектор произвольных постоянных.

Будем искать решение неоднородной системы в том же виде, варьируя вектор произвольных постоянных:

.

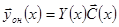Вычисляем производную и подставляем в уравнение неоднородной системы:

,

,

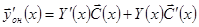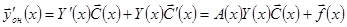Так как фундаментальная матрица удовлетворяет уравнению однородной системы, то 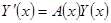. Поэтому в предыдущем уравнении (как и всегда в методе вариации) сокращается пара слагаемых. Получаем уравнение

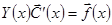. Так как фундаментальная матрица не вырождена (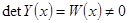), то отсюда получаем уравнение для определения вектора :

.

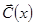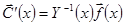Интегрируя, получаем

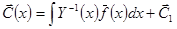(здесь предполагается, что при вычислении интеграла вектор констант не добавляется, он уже добавлен в виде вектора ).

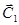Подставляя в 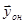, имеем

() .

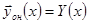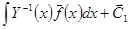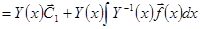Здесь в полном соответствии с теоремой о структуре общего решения неоднородной системы первое слагаемое представляет собой общее решение однородной системы, а второе слагаемое – частное решение неоднородной системы.

Дата добавления: 2015-04-24