Лекция 22. Однородные системы линейных дифференциальных уравнений с постоянными коэффициентами

Система линейных дифференциальных уравнений с постоянными коэффициентами может быть записана в ви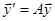де

, где 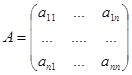, 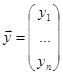(векторная форма записи)

или

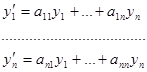(покоординатная форма записи).

Будем искать решение системы в виде .

Подставляя 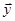в уравнение системы, получаем

.

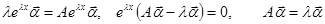Получено уравнение для определения соответствующего собственному значению 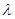собственного вектора линейного оператора с матрицей 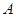. Система уравнений

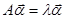или

имеет ненулевое решение только, когда определитель системы равен нулю, т.е.

.

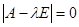Это – характеристическое уравнение системы линейных дифференциальных уравнений с постоянными коэффициентами. В развернутом виде его можно записать так:

.

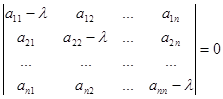Характеристическое уравнение представляет собой алгебраическое уравнение 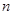- го порядка относительно 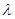. Из основной теоремы высшей алгебры известно, что оно имеет ровно 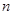корней. Часть корней может быть действительными корнями, часть - комплексными, но комплексные корни встречаются только парами комплексно-сопряженных корней. Это следует из действительности коэффициентов характеристического уравнения и теорем Виета.

1. Рассмотрим случай, когда все собственные значения 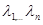линейного оператора с матрицей 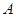(или все характеристические числа матрицы 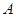, что одно и то же) действительны и различны.

Из линейной алгебры известно, что действительным различным собственным значениям 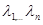соответствуют линейно независимые собственные векторы , которые можно определить по собственным значениям из системы уравнений

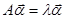или .

В развернутом виде эти уравнения для 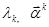можно записать в виде

.

Теперь решения системы линейных однородных уравнений с постоянными коэффициентами будут

.

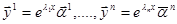Проверим, что решения являются линейно независимыми. Составим определитель Вронского

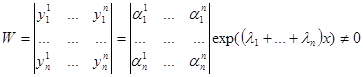, так как векторы линейно независимы и определитель из координат этих векторов отличен от нуля. Так как определитель Вронского отличен от нуля, то полученные решения линейно независимы. Так как этих решений ровно n, то они составляют фундаментальную систему решений. Следовательно, общее решение системы линейных однородных уравнений может быть записано в виде

.

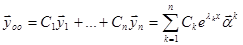Пример. , ,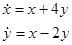

,

,

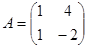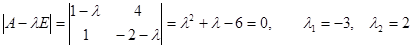
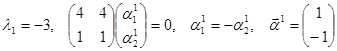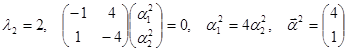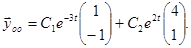
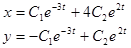
2. Рассмотрим случай, когда среди корней характеристического уравнения имеются s простых корней .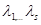

Этот случай легко свести к предыдущему. Для каждого собственного значения (характеристического числа) отыщем собственный вектор 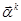из системы уравнений

.

Затем найдем соответствующие им решения из фундаментальной системы решений 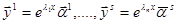и запишем общее решение в виде

..

Вся разница с предыдущим случаем в том, что фундаментальная система решений не исчерпывается найденными решениями, есть еще решения, соответствующие другим корням характеристического уравнения.

3. Среди корней характеристического уравнения имеется простая пара комплексно сопряженных корней .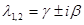

Справедливо утверждение, которое мы примем без доказательства: простой паре комплексно сопряженных корней 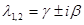соответствует пара комплексно сопряженных собственных векторов .

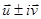Запишем формально соответствующую пару решений:

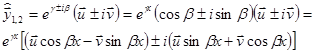
Эти решения комплексные. Вместо них мы (по линейности и теоремам о свойствах решений) можем взять решения Общее решение можно записать в виде:

..

Пример.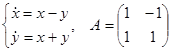

.

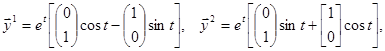
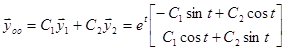
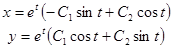
4. Среди корней характеристического уравнения встречаются кратные действительные корни или кратные пары комплексно сопряженных корней.

Этот случай мы не можем рассмотреть подробно, так как пока в курсе математики для инженеров не рассматривается жорданова форма матрицы, а именно к матрице с жордановыми клетками в общем случае приводится матрица системы (хотя матрица может привестись и к диагональному виду, и проблемы это не снимает). Укажем только алгоритм действий для действительного корня (или пары комплексно сопряженных корней) кратности r. Алгоритм этот основан на двух теоремах.

Теорема. Существует система из n линейно независимых векторов

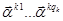, удовлетворяющих соотношениям

.

Векторы 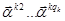- присоединенные векторы, порожденные собственным вектором 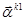, - кратность корня , сумма для различных корней равна n.

Теорема. Каждому корню соответствует решений вида

……………………….

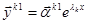
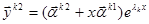
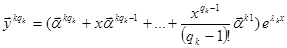
Для каждого кратного корня надо найти присоединенные векторы по первой теореме и построить решения по второй теореме.

Если порядок системы мал, то можно действовать проще.

Пусть матрица 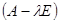для корня, кратности 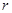будет иметь ранг .

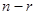Это означает, что для данного корня можно подобрать r линейно независимых собственных векторов и, соответственно, r линейно независимых решений вида 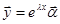в фундаментальной системе решений.

Пример. , .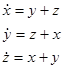

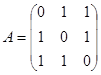Заметим, что матрица симметрическая, она приводится к диагональному виду ортогональным преобразованием. Следовательно, собственные векторы можно выбрать ортогональными, так как именно в базисе из собственных векторов матрица имеет диагональный вид, а ортогональное преобразование переводит один ортонормированный базис в другой.

Запишем характеристическое уравнение и найдем его корни.

.

.

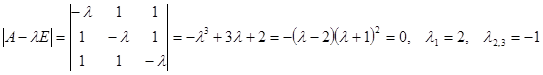
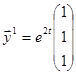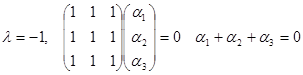. Кратность корня равна 2. Ранг матрицы равен n-r = 3 – 2 = 1. Из полученного уравнения можно выбрать координаты двух линейно независимых векторов. Например,

. Тогда .

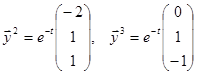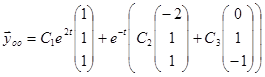или

.

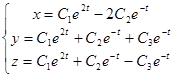Если действительному корню кратности r соответствует m(m<r) линейно независимых собственных векторов, то решение надо искать в виде

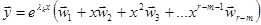. Координаты векторов 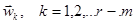отыскиваются путем подстановки решения в систему дифференциальных уравнений и приравнивания коэффициентов при одинаковых степенях x.

Пример.

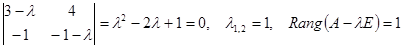
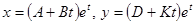. Подставим x, y в систему уравнений, приравняем коэффициенты при в каждом уравнении, получим систему уравнений для определения неопределенных коэффициентов

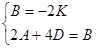, откуда получим . Можно выбрать, например,

1) 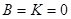, , 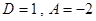тогда 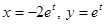или

2) 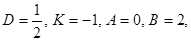тогда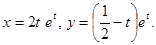

Лекции 23-24. Устойчивость движения, классификация точек покоя, теоремы Ляпунова.

Рассмотрим нелинейную систему дифференциальных уравнений, запишем ее уравнения в векторной форме

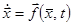
или в координатной форме

.

В качестве независимой переменной выбрано время t, поэтому система дифференциальных уравнений является моделью некоторого процесса – изменения переменной 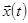во времени или движения материальной точки, занимающей в фазовом пространстве текущее положение 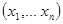и изменяющей это положение с изменением времени t. Таким образом, движение – это частное решение системы дифференциальных уравнений.

Зададим некоторые начальные условия 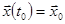. Пусть выполняются условия теоремы Коши (непрерывны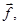 в рассматриваемой области). Тогда через любую точку расширенного фазового пространства 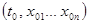из рассматриваемой области проходит единственная интегральная кривая – график частного решения 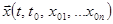. Назовем движение, «начинающееся» в точке 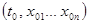невозмущенным движением 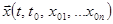. Если «возмутить» – несколько изменить начальные условия в фазовом пространстве, выбрать их 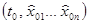, то изменится и движение. Назовем движение, «начинающееся» в точке 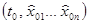, возмущенным движением . Если возмущение начальных условий невелико, то в некоторой окрестности начальной точки траектории – движения тоже близки.

Справедлива теорема о непрерывности решения по начальным условиям. Пусть выполнены условия теоремы Коши. Тогда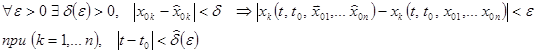

Отсюда видно, что близость возмущенного и невозмущенного движений гарантируется в некоторой временной окрестности, размер которой зависит от размеров трубки – окрестности («допуска») в фазовом пространстве координат.

Однако в практике встречаются процессы, для которых надо гарантировать близость возмущенного и невозмущенного движений «вообще», при любом времени t > T (важно, чтобы существовало это некоторое T).

Например, запустив спутник на орбиту, полезно быть уверенным, что он не свалится нам на голову через 10 или 100 лет, а будет «вечно» находиться на орбите.

В наше время приходится сталкиваться с экологическими проблемами. Кто же знал, конструируя двигатель внутреннего сгорания, что через некоторое время использование этого открытия поставит под угрозу существование жизни на Земле?

Рассматривая близость возмущенного и невозмущенного движений «вообще», при любом времени t > T, мы приходим к определению устойчивости движения по Ляпунову.

Движение называется устойчивым по Ляпунову, если

Смысл определения в том, что для любого размера окрестности «допуска» (по фазовым координатам) невозмущенного движения существует размер окрестности, в которой можно «возмутить» начальные условия. Причем это возмущение приведет к тому, что возмущенное движение после некоторого момента времени Т войдет в окрестность «допуска» и останется в этой окрестности при любом t > T.

Если движение устойчиво по Ляпунову и 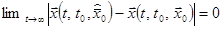, то такое движение называется асимптотически устойчивым.

Если движение асимптотически устойчиво, то возмущенное движение с ростом времени стремится к невозмущенному.

Движение называется неустойчивым по Ляпунову, если

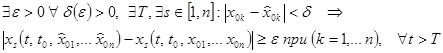
Смысл этого определения в том, что как бы ни было мало возмущение начальных условий, все равно со временем хотя бы по одной координате возмущенное движение выйдет из некоторой окрестности «допуска» невозмущенного движения.

Теорема. Задача об устойчивости движения может быть сведена к задаче об устойчивости тривиального (тождественно равного нулю) решения системы.

Доказательство. Обозначим 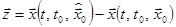. Тогда

.

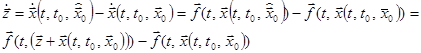При 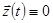имеем 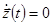, поэтому задача об устойчивости движения для исходной системы уравнений может быть заменена эквивалентной ей задачей об устойчивости тривиального решения для системы

.

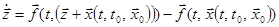Поэтому обычно заранее делают указанную замену и исследуют задачу об устойчивости тривиального решения.

Таким образом, задача об устойчивости движения может быть сведена для автономной системы к исследованию характера ее точки покоя 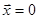(при рассмотрении свойств автономных систем было показано: если 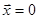- точка покоя, то - решение системы).

Дата добавления: 2015-04-24