Точка покоя

Система второго порядка.

Запишем уравнение автономной системы второго порядка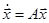

1. Корни характеристического уравнения 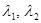действительны..

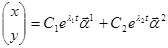
а) .

При 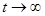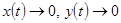. Поэтому точка покоя (или тривиальное решение) асимптотически устойчива.

Заметим, что первое слагаемое – это проекция траектории на ось 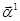, второе слагаемое – проекция на ось .

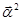Такая точка покоя называется

устойчивый узел.

б) .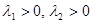

Этот случай можно рассматривать как предыдущий, если формально положить t < 0. Получим те же траектории, что и в п. а), но стрелки на них будут направлены в другую сторону. Направление движение другое (t<0). Такая точка называется неустойчивый узел.

в) .

По вектору 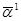мы, находясь на траектории, стремимся к нулю, по вектору 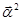, наоборот, удаляемся от нуля.

Такая точка покоя - седло.

г) .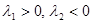

Это – тоже седло, но стрелки

направлены в другую сторону.

Траектория прижимается к той оси, для которой модуль характеристического числа меньше.

Седла – неустойчивые точки покоя.

Заметим, в ситуациях узлов и седла траектория, начавшись в определенном квадранте, в нем и остается.

д) .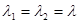

Точка покоя – дикритический узел,

Устойчивый при 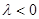, неустойчивый при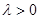

е)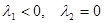

Точка покоя - вырожденный узел, при 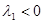устойчивая, но не асимптотически устойчивая. Если 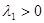, то точка покоя - неустойчивая (стрелки направлены в обратную сторону)

ж) 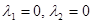. Точка безразличного равновесия. При изменении времени любая точка остается на месте. Этими точками заполнена вся плоскость.

2. Корни характеристического уравнения комплексно сопряженные.

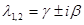
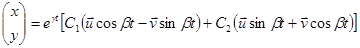
Параметр t имеет смысл угла поворота вокруг начала координат (в периодической составляющей).

а) Если 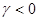, то траектория приближается к началу координат с ростом t (спираль), так как 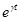- убывающая функция. Точка покоя устойчивый фокус асимптотически устойчива

б) если 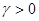, то траектория удаляется от начала координат с ростом t (спираль), так как 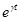- возрастающая функция. Точка покоя неустойчивый фокус неустойчива

в) если 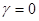, то траектории представляют собой эллипсы, охватывающие начало координат. Точка покоя центр устойчива, но не асимптотически устойчива.

а) б) в)

Пример. , ,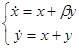

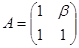Классифицировать точки покоя в зависимости от параметра.

,

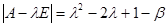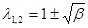
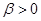
а) 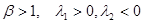седло,

б) 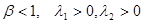неустойчивый узел

в) 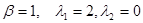вырожденный узел

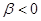
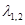- комплексно сопряженные.

Так как 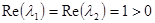, то точка покоя – неустойчивый фокус

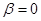
3) 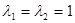, точка покоя – неустойчивый дикритический узел.

Дата добавления: 2015-04-24