Формулы для расчетов

Конус	Пирамида	Призма
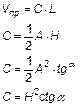
Клин	Обелиск

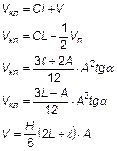
Общими для этих фигур являются соотношения:

Второй метод – метод коэффициентов формы – заключается в том, что объем штабелей правильной геометрической формы определяется по формуле

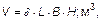
где 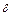– коэффициент формы. Он разный для разных фигур.

Объем конуса:

Объем пирамиды:

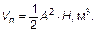
Объем призмы:

Объем клина:

Объем обелиска:

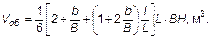
Для определения объема штабелей правильной формы Л.П. Андроновым предложена номограмма (рис. 3.2).

tga

Рис. 3.2. Номограмма для определения объема штабелей навалочных грузов

Она состоит из девяти логарифмических шкал на пяти осях и дает возможность определить все остальные элементы, если известны хотя бы два, например, угол естественного откоса и периметр основания конуса .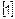

Шкалы 5, 6, 8 предназначены для определения объема призмы.

Для определения объема конуса измеренные значения диаметра (или окружности основания) и угла откладывают на шкалах 1(2) и 9, соединяют эти точки прямой и со шкалы 4 снимают его значение. Если значения А или S выходят за пределы шкал, то их уменьшают в 10 раз, а результат на шкале 4 увеличивают в 10³ раз.

Объем пирамиды определяют аналогично (по шкалам 1, 9 и 3). Для определения объема призмы откладывают измеренные значения на шкалах 1 и 9, соединяют эти точки прямой, пересечение которой со шкалой 5 дает значение С. Точка пересечения прямой, проведенной между значением на шкале С и значением L, отложенным на шкале 8, со шкалой 6 дает значение объема V_пр призмы. Если значение величины выходит за пределы шкалы 8, его уменьшают в 10 (100) раз, соответственно увеличивают значение V_пр.

При определении объема клина по значениям А и 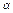находят объем V_п пирамиды (или конуса, если основание круглое) и значение величины С, по С и L – объем V_пр призмы. Объем клина равен сумме объемов пирамиды V_п (конуса V_к) и призмы V_пр.

Объем обелиска можно представить как сумму объемов параллелепипеда l b Н (см. рис. 3.1, д), призмы сечением С, длиной (L + B) и пирамиды (конуса, если основание круглое), высота которой равна высоте обелиска. Для определения V_об надо знать значения L и l, В и b, угол 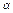либо Н. По разности соответствующих сторон оснований определяют сторону основания пирамиды (диаметр конуса), по длине и ширине основания – длину призмы. Значения величин Н, С, V_п (V_к) находят по номограмме (см. рис. 3.2) на шкалах А и .

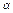На шкале 1 откладывают значение А = В – в, на шкале 9 – значение 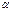. Соединив полученные точки прямой, получают на шкале 3 значение V_п, на шкале 5 – значение С, на шкале 7 – значение высоты Н обелиска. На шкале 8 откладывают значение L. Соединив полученную точку с точкой С на шкале 6, снимают значение объема V_пр призмы. Объем обелиска V_об = V_пр + V_п + ℓb H.

Дата добавления: 2015-03-29