Сложение взаимно перпендикулярных колебаний

Сначала рассмотрим случай, когда частоты складываемых колебаний одинаковы. Пусть координаты х и у частицы изменяются по закону

(23)

Можно показать, что траекторией частицы при этом является эллипс (рис.10), вид которого определяется отношением амплитуд a и b и разностью фаз d.

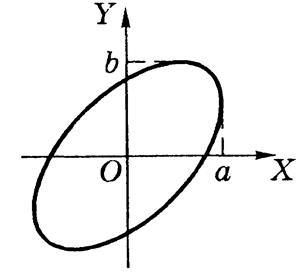
Рис.10

Некоторые частные случаи:

а) d = 0, тогда y = (b / a) x, т.е. частица движется по прямой в первом и третьем квадрантах (рис.11, а);

б) d = p, тогда y = — (b / a) x и частица движется тоже по прямой, но во втором и четвертом квадрантах (рис.11, б);

в) d = p/2. В этом случае x ²/ a ² + y ²/ b ² = 1, т.е. частица движется по эллипсу, полуоси которого а и b совпадают с осями координат. При а = b эллипс превращается в окружность. Так как колебания вдоль оси У происходят с опережением по фазе на p/2 относительно колебаний по оси Х, то сначала у и лишь затем х достигают максимальных значений. Это значит, что движение частицы будет происходить по часовой стрелке (рис.11, в);

г) d = 3p/2. Это то же, что и d = —p/2, поскольку изменение фазы на 2p несущественно (рис.11, г).

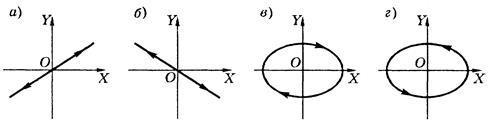
Рис.11

Если частоты взаимно перпендикулярных колебаний не одинаковы и относятся как целые числа, то траектории результирующего движения имеют более сложные формы. Их называют фигурами Лиссажу. Одна из этих фигур показана на рис.12, она соответствует отношению частот

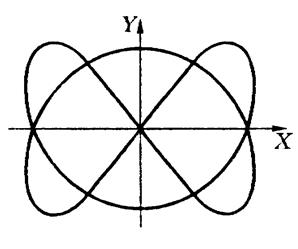
Рис.12

И последнее: при сложении взаимно перпендикулярных колебаний полная энергия

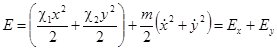, (24)

т.е. складывается изэнергий каждого колебания (в отличие от сложения колебаний одного направления(. Согласно (13), эта энергия

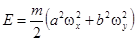. (25)

Дата добавления: 2015-04-24