Формулы логики высказываний. Равносильность формул

Логическая формула – запись сложного высказывания в виде простых высказываний, соединенных операциями отрицания, конъюнкции, дизъюнкции, импликации, эквиваленции и скобок.

В случае, если в логической формуле присутствуют несколько операций, не разделенных скобками, то порядок выполнения операций следующий:

1) отрицание;

2) конъюнкция;

3) дизъюнкция;

4) импликация;

5) эквиваленция.

Формула называется тавтологией, если она истинна при любых значениях истинности, входящих в нее высказываний.

Например, рассмотрим возможные значения истинности формулы . Построим таблицу истинности для данной формулы.

А	В

Формула всегда только истинна, значит является тавтологией.

Формула называется противоречием, если она ложна при любых значениях истинности, входящих в нее высказываний.

Например, рассмотрим возможные значения истинности формулы 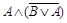. Построим таблицу истинности для данной формулы.

А	В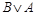

Формула всегда только ложна, значит является противоречием.

Формулы называются равносильными, если при любых значениях истинности высказываний, в них входящих, значения истинности формул совпадают.

Для обозначения равносильности формул используют знак 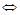. Для выяснения равносильности формул для них строят таблицы истинности.

Например, доказать равносильность формул 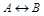и .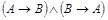

Отразим в таблице истинности значения истинности каждой формулы.

А	В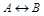

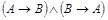
Значения истинности формул при одинаковых значениях истинности высказываний А и В совпадают (выделенные столбцы), что дает право утверждать равносильность формул, значит .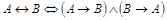

Аналогично можно показать, что имеют место следующие равносильности, которые называют законами логики:

1. (закон двойного отрицания);

2. 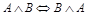(закон коммутативности конъюнкции);

3. (закон коммутативности дизъюнкции);

4. (закон ассоциативности конъюнкции);

5. (закон ассоциативности дизъюнкции);

6. (закон дистрибутивности конъюнкции относительно дизъюнкции);

7. 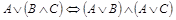(закон дистрибутивности дизъюнкции относительно конъюнкции);

8. 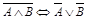(закон де Моргана);

9. (закон де Моргана);

10. 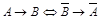(закон контрапозиции);

11. (закон поглощения);

12. 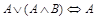(закон поглощения);

13. ;

14. ;

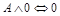15. ;

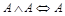16. (закон противоречия);

17. ;

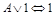18. ;

19. ;

20. (закон исключенного третьего);

Дата добавления: 2015-04-24