
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общие правила комбинаторики
|
|
|
|
Комбинаторные задачи – задачи о комбинациях каких-либо объектов. При составлении комбинации приходится из предоставленного множества выбрать определенное количество элементов.
Существуют два принципиально различных способа выбора некоторого числа элементов из заданного множества:
· выбор без повторения (без возвращения), т.е. отобранные элементы исключаются из множества;
· выбор с повторением (с возвращением), т.е. отбор производится поэлементно с обязательным возвращением отобранного элемента в исходное множество перед выбором следующего.
В более сложных ситуациях могут быть полезными правила, которые мы рассмотрим на следующем примере.
Пример:
В магазине 5 видов коробок конфет и 4 вида коробок печенья. Сколькими способами можно купить в подарок: а) коробку конфет или коробку печенья; б) набор из коробки конфет и коробки печенья?
Решение: а) Коробку конфет можно выбрать пятью способами, а коробку печенья – четырьмя способами. Следовательно, коробку конфет или коробку печенья можно выбрать 5 + 4 = 9 способами.
б) Будем составлять наборы из коробки конфет и коробки печенья. С первым видом коробки конфет возможно 4 варианта подарка (с каждым из четырех видов коробок печенья), со вторым видом коробок конфет аналогично 4 варианта и т.д. Следовательно, с каждым из пяти видов коробок конфет возможно по 4 варианта подарка. Итого 5*4=20 способов купить подарок.
Правило произведения. Если некоторый объект А можно выбрать m способами, а объект В – k способами, то объект «А и В» можно выбрать (  ) способами.
) способами.
Пример:
Сколькими способами можно выбрать 3 шара из 8 (без возвращения)?
Решение: Первый шар можно выбрать восьмью способами, второй – семью способами, а третий – шестью способами. Тогда три шара можно выбрать  способами.
способами.
Правило суммы. Если объект А можно выбрать m способами, а объект В – k способами (выбор объекта А и объекта В - взаимоисключающие действия), то объект «А или В» можно выбрать (m+k) способами.
Пример:
В группе 20 человек – 12 девушек и 8 юношей. Сколькими способами можно выбрать двух человек одного пола?
Решение: Можно выбрать двух юношей или двух девушек. Двух девушек можно выбрать  способами, двух юношей
способами, двух юношей 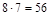 способами. Тогда выбрать двух человек одного пола можно выбрать 132 + 36 = 168 способами.
способами. Тогда выбрать двух человек одного пола можно выбрать 132 + 36 = 168 способами.
3.2. Размещения, сочетания и перестановки
без повторения (без возвращения)
Пусть дано множество  , состоящее из n различных элементов. Из Е будем выбирать m элементов без повторения (без возвращения) последовательно по одному. Будем получать m -элементные подмножества множества Е (
, состоящее из n различных элементов. Из Е будем выбирать m элементов без повторения (без возвращения) последовательно по одному. Будем получать m -элементные подмножества множества Е ( ).
).
А) Если при этом порядок следования элементов важен, то будем получать упорядоченные m -элементные подмножества множества Е, отличающиеся друг от друга либо набором элементов, либо порядком их следования. Такие комбинации называют размещениями из n элементов по m без повторения (без возвращения). Их количество вычисляется по формуле:
 .
.
Замечание: Для любого натурального n можно вычислить n -факториал по формуле: 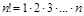 . При чем, принято считать,
. При чем, принято считать, 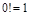 .
.
Пример:
Имеется 10 футбольных команд. Сколькими способами можно провести награждение этих команд медалями (золотой, серебряной и бронзовой)?
Решение: Из 10 команд нужно выбрать 3. Значит 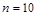 , а
, а 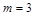 . При этом
. При этом  . Порядок следования элементов важен, т.к. если одни и те же элементы брать в разном порядке, то будем получать отличные варианты награждения. Кроме того, награжденная команда исключается из исходного множества команд (выбор без возвращения). Значит, полученные комбинации являются размещениями из 10 по 3 без возвращения. Количество таких комбинаций:
. Порядок следования элементов важен, т.к. если одни и те же элементы брать в разном порядке, то будем получать отличные варианты награждения. Кроме того, награжденная команда исключается из исходного множества команд (выбор без возвращения). Значит, полученные комбинации являются размещениями из 10 по 3 без возвращения. Количество таких комбинаций: 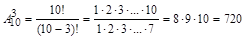 . Итак, 720 способов.
. Итак, 720 способов.
Б) Если при этом порядок следования элементов не важен, то будем получать m -элементные подмножества множества Е, отличающиеся друг от друга только набором элементов. Такие комбинации называют сочетаниями из n элементов по m без повторения (без возвращения). Их количество вычисляется по формуле:
 .
.
Пример:
В группе 10 человек. Сколькими способами можно выбрать 3 дежурных?
Решение: Из 10 человек нужно выбрать 3. Значит 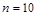 , а
, а 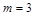 . При этом
. При этом  . Порядок следования элементов не важен, т.к. трое отобранных дежурных могут быть выбраны в разном порядке – суть от этого не меняется. Кроме того, выбранный дежурный исключается из исходного множества и не может быть выбранным снова (выбор без возвращения). Значит, полученные комбинации являются сочетаниями из 10 по 3 без возвращения. Количество таких комбинаций:
. Порядок следования элементов не важен, т.к. трое отобранных дежурных могут быть выбраны в разном порядке – суть от этого не меняется. Кроме того, выбранный дежурный исключается из исходного множества и не может быть выбранным снова (выбор без возвращения). Значит, полученные комбинации являются сочетаниями из 10 по 3 без возвращения. Количество таких комбинаций:  . Итак, 120 способов.
. Итак, 120 способов.
Напомним, что имеем множество  , состоящее из n различных элементов. Будем задействовать в комбинации все n элементов множества Е, получая при этом множества состоящие из различных элементов, т.е. комбинации без повторения и отличающиеся друг от друга только порядком следования элементов. Таким образом, получим размещениями без повторения, но
, состоящее из n различных элементов. Будем задействовать в комбинации все n элементов множества Е, получая при этом множества состоящие из различных элементов, т.е. комбинации без повторения и отличающиеся друг от друга только порядком следования элементов. Таким образом, получим размещениями без повторения, но  , т.е.
, т.е.  Такие комбинации называют перестановками из n элементов без повторения. Их количество вычисляется по формуле:
Такие комбинации называют перестановками из n элементов без повторения. Их количество вычисляется по формуле:
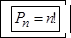
Пример:
Сколькими способами могут встать в очередь 5 студентов?
Решение: Из 5 студентов нужно задействовать в комбинации всех 5 студентов. Значит, в комбинации использованы все предоставленные элементы. Выбранный и поставленный в очередь студент исключается из исходного множества и не может быть выбранным снова (выбор без повторения). Значит, полученные комбинации являются перестановками из 5 элементов без повторения. Количество таких комбинаций: 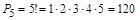 . Итак, 120 способами могут встать в очередь 5 студентов.
. Итак, 120 способами могут встать в очередь 5 студентов.
3.3. Размещения, сочетания и перестановки
с повторением (с возвращением)
Пусть дано множество  , состоящее из n различных элементов. Из Е будем выбирать m элементов с повторением (с возвращением) последовательно по одному. Будем получать m -элементные подмножества множества Е (
, состоящее из n различных элементов. Из Е будем выбирать m элементов с повторением (с возвращением) последовательно по одному. Будем получать m -элементные подмножества множества Е ( ).
).
А) Если при этом порядок следования элементов важен, то будем получать упорядоченные m -элементные подмножества множества Е, отличающиеся друг от друга либо набором элементов, либо порядком их следования. Такие комбинации называют размещениями из n элементов по m с повторением (с возвращением). Их количество вычисляется по формуле:
 .
.
Пример:
Сколько различных трехзначных чисел можно составить, используя цифры 2, 4, 6, 7, 9?
Решение: Чтобы составить трехзначное число из 5 цифр нужно выбрать 3. Значит  , а
, а 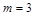 . При этом
. При этом  . Порядок следования элементов важен, т.к. если выбрать одни и те же цифры, но в разном порядке, то будем получать отличные друг от друга числа. Кроме того, выбранная цифра может в числе встретиться не один раз, значит выбор с повторением (с возвращением). Значит, полученные комбинации являются размещениями из 5 по 3 с возвращением. Количество таких комбинаций:
. Порядок следования элементов важен, т.к. если выбрать одни и те же цифры, но в разном порядке, то будем получать отличные друг от друга числа. Кроме того, выбранная цифра может в числе встретиться не один раз, значит выбор с повторением (с возвращением). Значит, полученные комбинации являются размещениями из 5 по 3 с возвращением. Количество таких комбинаций: 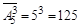 . Итак, 125 трехзначных чисел можно составить, используя цифры 2, 4, 6, 7, 9.
. Итак, 125 трехзначных чисел можно составить, используя цифры 2, 4, 6, 7, 9.
Б) Если при этом порядок следования элементов не важен, то будем получать m -элементные подмножества множества Е, отличающиеся друг от друга только набором элементов. Такие комбинации называют сочетаниями из n элементов по m с повторением (с возвращением). Их количество вычисляется по формуле:
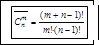 .
.
Пусть во множестве  встречаются одинаковые элементы. Допустим, элемент
встречаются одинаковые элементы. Допустим, элемент  встречается
встречается  раз, элемент
раз, элемент 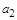 встречается
встречается  раз и т.д. (пусть при этом во множестве F t различных элементов). Будем задействовать в комбинации все n элементов множества F, получая при этом комбинации, отличающиеся друг от друга только порядком следования элементов. Такие комбинации называют перестановками из n элементов с повторением. Их количество вычисляется по формуле:
раз и т.д. (пусть при этом во множестве F t различных элементов). Будем задействовать в комбинации все n элементов множества F, получая при этом комбинации, отличающиеся друг от друга только порядком следования элементов. Такие комбинации называют перестановками из n элементов с повторением. Их количество вычисляется по формуле:

Пример:
На карточках написаны буквы, образующие слово «математика». Их перемешивают и выкладывают в ряд. Сколько различных вариантов это сделать?
Решение: Из 10 карточек нужно задействовать в комбинации все 10. Значит, в комбинации использованы все предоставленные элементы. Среди 10 букв некоторые встречаются несколько раз, значит комбинации с повторениями и являются перестановками. Количество таких комбинаций:  . Ответ: 151200 способов.
. Ответ: 151200 способов.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1120; Нарушение авторских прав?; Мы поможем в написании вашей работы!