Числовые характеристики случайных величин. Математическим ожиданием случайной величины Х называется среднее значение

Математическим ожиданием случайной величины Х называется среднее значение

для дискретной случайной величины: , (2.20)

для непрерывной случайной величины: 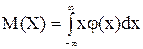, (2.21)

Дисперсия случайной величины Х – математическое ожидание квадрата отклонения случайной величины от её математического ожидания

для дискретных случайных величин 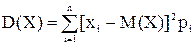, (2.22)

для непрерывных случайных величин , (2.23)

или , (2.24)

где, М[X²] – математическое ожидание квадрата отклонения случайной величины от математического ожидания М(Х),

для дискретных случайных величин 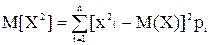, (2.25)

для непрерывных случайных величин 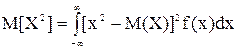,(2.26).

Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых

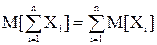, (2.27)

Дисперсия суммы независимых случайных величин выражается формулой

, (2.28)

Среднеквадратичной отклонение– корень квадратный из дисперсии

(2.29)

Нормальный закон распределения (закон Гаусса)

Случайная величина Х имеет нормальное распределение (или распределена по нормальному закону), если её плотность

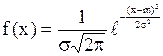, (2.30)

Математическое ожидание случайной величины, имеющей распределение (2.30), равно m, дисперсия s², среднее квадратичное отклонение s. Вероятность попадания случайной величины Х, имеющей нормальное распределение с параметрами m и s, на участок от a до b выражается формулой

, (2.31)

где Ф(Х)- интегральная нормированная функция распределения (функция Лапласа)

. (2.32)

Функция Лапласа обладает свойствами:

1) Ф(0)=0; 2) Ф(–х)=–Ф(х) (нечетная функция); 3) Ф(¥)=0,5. Значения функции Лапласа даны в табл. 1.

Если участок (a, b) симметричен относительно точки m, то вероятность попадания в него

, (2.33)

где 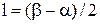– половина длины участка.

Нормальное распределение возникает тогда, когда величина Х образуется в результате суммирования большого числа независимых (или слабо зависимых) случайных слагаемых, сравнимых по своему влиянию на рассеивание суммы.

Значения функции Лапласа

Таблица 1.

X						б	в
0,0	0,00000
0,1
0,2				09095:
0,3								.14431
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1							37G98
1,2						39^35
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5		49396-
2,6									.49632
2,7
2,8
2,9
3,0 3,5 4,0 4,5 5,0	0,49865	3,1 3,6	49903 49984	3,2 3,7	49931 49989	3,3 3,8	49952 49993	3,4 3,9	49966 49995

Дата добавления: 2015-04-24