З а д а ч а 4

З а д а ч а 3

Построить тени на цилиндрической оболочке (рис. 30).

При заданном направлении светового потока S часть наружной
и внутренней поверхности оболочки освещена, а границей освещенности будет левая очерковая образующая цилиндрической поверхности, проходящая через точку (4, 4'). На внутренней поверхности, на эпюре тень выделена бледным цветовым оттенком.

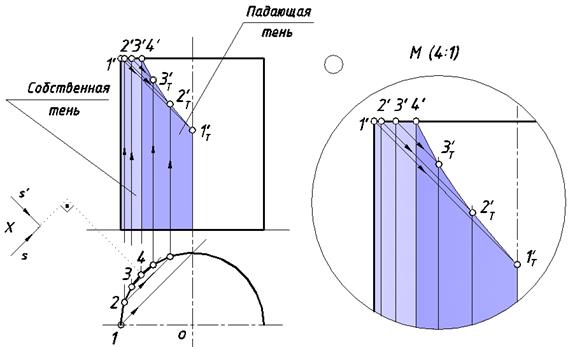
Рис. 30. Собственная и падающая тень цилиндрической оболочки

Часть дуги верхней дуги окружности от точки (1, 1') до (4, 4') находится на границе света и тени, следовательно, входит в состав контура собственной тени оболочки. Через каждую точку этой дуги проходит световой луч. Множество лучей образует поверхность эллиптического цилиндра. Ее пересечение с внутренней поверхностью оболочки – кривая четвертого порядка. Для построения этой кривой через вышеуказанные точки проводим световые лучи и отмечаем их пересечение с внутренней поверхностью. Полученные точки 1_Т', 2_Т', 3_Т' и 4_Т' соединяем плавной кривой – это падающая тень верхней дуги окружности. Лучевая горизонтально-проецирующая плоскость, проходящая через левую очерковую образующую, пересекает внутреннюю поверхность оболочки по прямой, ей параллельной, которая является ее падающей тенью.

Построить тень отрезка [ AB ] на поверхности цилиндрической оболочки (рис. 31).

Нахождение теней оболочки показано в предыдущей задаче, поэтому на чертеже, приведенном ниже, построения не показаны.

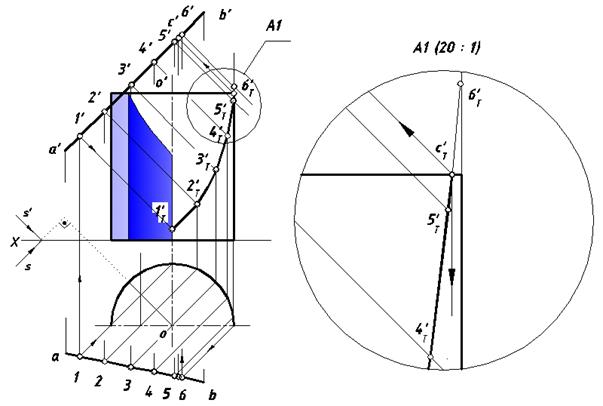
Рис. 31. Падающая тень отрезка [ AB ] на цилиндрическую оболочку

Для решения этой задачи использовано свойство проецирующей цилиндрической поверхности.

Множество лучей, проходящих через отрезок [ AB ], образует лучевую плоскость. Поскольку она является плоскостью общего положения
и пересекает все образующие цилиндрической оболочки, то результатом пересечения этих образов (тенью) будет эллипс (или часть его дуги).

Ввиду того, что эллипс это лекальная кривая, ее построение выполняется по множеству точек. Возьмем на отрезке [ AB ] точку (1, 1'). Это первая левая точка на данном отрезке, которая заведомо отбросит тень на внутреннюю поверхность оболочки.

Точки, расположенные на отрезке влево от нее, отбрасывают тени на наружную часть цилиндрической поверхности, которая на фронтальной проекции не видна ввиду своей непрозрачности, поэтому их тени строить не имеет смысла.

Проведем через точку (1, 1') луч, параллельный S и отметим его пересечение с цилиндрической поверхностью – действительную тень 1_Т'. Затем на отрезке [ AB ] возьмем случайные точки (2, 2'), (3, 3'), … (6, 6') и выполним аналогичные построения. Заметим, что точка 6_Т' оказалась за пределами левой очерковой образующей оболочки. Соединим построенные точки плавной кривой. Заметим, что точка С (с, c’), отбрасывающая тень на окружность верхнего основания цилиндра, может быть найдена лишь приближенно после построения эллиптической дуги по множеству случайных точек.

Для построения теней от одного объекта на другой инженеры-строители применяют следующие приемы:

метод секущих плоскостей;

метод обратного луча.

Архитекторы используют для своих целей девять различных способов (в данной работе они не приводятся).

Рассмотрим метод секущих плоскостей, который заключается
в следующем. Заданные геометрические объекты рассекаются вспомогательными плоскостями, параллельными световому лучу и перпендикулярными к какой-либо плоскости проекций. Затем определяются линии сечения каждого объекта вспомогательными плоскостями. Плоское сечение первого объекта необходимо для определения лучей, касательных к его поверхности. Пересечение этих лучей с поверхностью другого объекта позволяет найти точки контура тени, падающей с одного объекта на другой.

Решение задачи, приведенной выше, можно объяснить, применяя метод секущих плоскостей.

Проведем вспомогательные плоскости, параллельные световому лучу и перпендикулярные плоскости H (на чертеже следы этих плоскостей не обозначены). Каждая из этих плоскостей пересекает отрезок [ AB ] в точке, а цилиндрическую поверхность по образующей. Проведя через построенные точки, лучи до пересечения с оболочкой, найдем их действительные тени, по которым найдем очертание контура падающей тени отрезка [ AB ].

В приводимых ранее задачах использовался метод обратных лучей. Приведем общие рекомендации по применению этого метода.

Метод обратных лучей заключается в том, что вначале строятся контуры падающих теней от заданных геометрических объектов (эти построения для решения задачи являются вспомогательными). Далее определяются точки пересечения полученных контуров. Из этих точек проводятся в пространстве лучи, направление которых противоположно лучам света. Точки встречи проекций обратных лучей с соответствующими проекциями первого объекта позволяют определить те точки, которые отбрасывают тени на другой объект.

Покажем решение предыдущей задачи с применением метода обратных лучей.

Построим падающие тени двух геометрических объектов на плоскости проекций независимо друг от друга. При нахождении последних использованы мнимые тени. На падающей тени отрезка взяты случайные точки, которым обеспечена принадлежность оболочки цилиндра его образующими. С помощью обратных лучей на отрезке [ AB ] определены точки, которые отбросили тени на другой объект. Заметим, что применение этого способа позволяет точно построить точку С (с, c’).

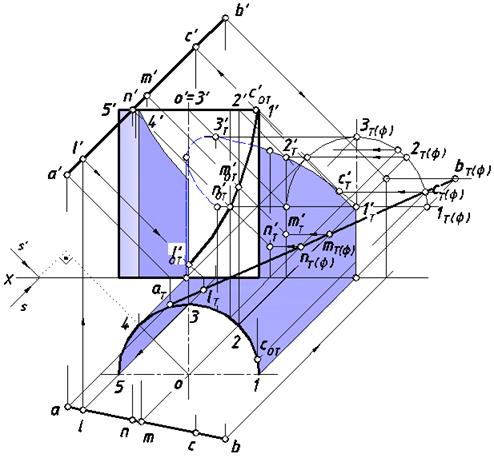
Рис. 32. Решение задачи с применением метода обратных лучей

На приведенных выше рисунках представлены решения задачи
с применением различных способов. В первом случае нельзя найти точное положение последней точки C (c, с’) отрезка [ AB ], которая отбросила тень на оболочку цилиндра, но можно обойтись без построений падающих теней. Применяя способ обратных лучей можно точно определить местонахождение точки C (c, с’),.но в этом случае, необходимо строить падающие тени.

6. 2. 2. Тень конического тела

Дата добавления: 2015-04-24