Порядок выполнения работы. Экспериментальная установка

Экспериментальная установка

Экспериментальная часть

Приборы и оборудование: доска Гальтона, сосуд с частицами (зерно, дробь), воронка, мензурка и линейка, коробочки для сбора частиц.

В работе используется механическая модель (доска Гальтона), в которой искусственно осуществляется одномерное рассеивание частиц. Сыпучий материал (зерно, дробь) засыпается через отверстие с помощью воронки. Внутри прибора в шахматном порядке расположены гвозди, играющие роль рассеивающих центров при движении частиц сверху вниз. В нижней части прибора сделаны ячейки шириной d =2 см, в которые попадают засыпаемые частицы. Ячейки пронумерованы 1¸11, рассеивающие центры находятся на расстоянии 0.5 см друг от друга, число рядов рассеивающих центров – 28. Рассеянное в результате столкновений с гвоздями зерно, собираясь в приемнике, дает представление о характере распределения случайных отклонений частиц от вертикали. Картина ступенчатого распределения зерна в секциях приемника хорошо описывается кривой нормального распределения.

Задание 1. Градуировка прибора.

1. По заданию преподавателя на листке бумаги отсчитать N0 зерен и поместить их в малую коробочку для засыпки в прибор.

2. Прибор – доску Гальтона – расположить горизонтально и выдвинуть переднюю подвижную стенку. После этого осторожно засыпать в одну из ячеек прибора, например 5 или 6, отсчитанное количество зерна. После этого подвижную стенку задвинуть и установить прибор вертикально.

3. С помощью линейки измерить высоту h ₀ зерна в ячейке. Результат записать в табл.11.2.

4. Освободить прибор от засыпанных частиц и сдвинуть вверх подвижную стенку. Когда зерно высыплется, стенку закрыть. Зерно из коробки осторожно пересыпать в мензурку, используя воронку.

Таблица 11.2

N 0	h 0, мм	V	N

Задание 2. Измерения.

1. По указанию преподавателя в мензурку, используя воронку, засыпать указанный объем зерна. Объем записать в табл. 11.2.

2. Вставить воронку в верхнее отверстие прибора и осторожно засыпать зерно из мензурки в прибор. Мензурку держать перпендикулярно передней или задней стенке прибора. Линейкой измерить высоты заполнения ячеек 1¸11. В крайних ячейках, где этого сделать нельзя, подсчитать число частиц, попавших туда.

3. Освободить прибор от зерна (см. п. 4 задания 1). С этим количеством зерна опыт проделать еще два раза, рассчитать средние высоты заполнения ячеек h _{i ср.}.

4. Перевести высоты h _{i ср.} в количество зерен, используя результаты градуировки.

5. Результаты занести в таблицу 11.3.

6. Оценить общее число зерен N =Σ N _i, записать в табл. 11.2.

Задание 3. Обработка результатов измерений.

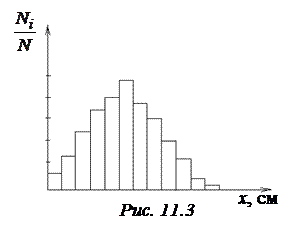
1. На миллиметровой бумаге построить две гистограммы: а) по оси абсцисс откладываются координаты x начала и конца ячейки; высота прямоугольника, построенного на этом основании, равна числу зерен N _i, попавших в i ^тую ячейку; б) по оси ординат откладывается доля (N _i/ N) частиц, попавших в i ^тую ячейку (см., например, рис.11.3).

2. Построить график, характеризующий заполнение ячеек: по оси ординат откладывается высота h _i зерна в ячейке, по оси абсцисс – координата x _i середины ячейки.

3. Построить график зависимости вероятности р_i=N _i/ N попадания частицы в данную ячейку от координаты середины ячейки x _i. Эта кривая должна достаточно хорошо приближаться к функции распределения Гаусса.

4. Рассчитать по формулам (11.6-11.8) и записать в таблицу 11.4 математическое ожидание, дисперсию и среднее квадратическое отклонение.

Таблица 11.3

Номера ячеек i
Координата середины ячейки x i, см
h i, мм
h i, мм
h i, мм
h i ср., мм
Число зерен в i ^той ячейке N i.
pi= N i/ N
f (x)

Таблица 11.4

, см	D, см^2	σ, см

5. Объяснить полученные результаты.

6. Используя полученные значения и σ, по формуле (11.16) рассчитать теоретические значения распределения Гаусса, записать в таблицу 11.3, сравнить с экспериментальными значениями вероятностей p_i, построить график функции f (x).

8. По окончании работы рабочее место привести в порядок.

Контрольные вопросы

1. Дайте определение вероятности, сформулируйте законы сложения и умножения вероятностей, приведите примеры.

2. Что такое математическое ожидание? При каком условии математическое ожидание совпадает со средним арифметическим?

3. Что такое дисперсия? Что она характеризует?

4. Что такое функция распределения вероятностей случайной величины? Что она показывает?

5. Чему равна площадь под графиком функции распределения?

6. Запишите закон Гаусса. Как изменится график нормального закона при изменении среднеквадратического отклонения?

7. Как, пользуясь графиком функции Гаусса, найти вероятность того, что случайная величина отклоняется от математического ожидания не больше, чем на Δ х?

8. Запишите закон распределения Максвелла по компонентам скоростей.

9. Как влияет на форму кривых распределения Максвелла температура?

10. Как изменятся форма кривых распределения частиц в механической модели и среднеквадратическое отклонение при увеличении количества рассеивающих центров (гвоздей)?

Используемая литература

[1] §§ 10.1, 10.2, 10.3, 10.4;

[2] §§ 35.1, 35.2, 35.3;

[3] §§ 5.42, 5.43, 5.44, 5.52;

[4] §§ 73,74;

[7] § 44.

Ла­бо­ра­тор­ная ра­бо­та 3-12

Дата добавления: 2015-03-29