Гитары сменных зубчатых колес

Гитара – это механизм со сменными зубчатыми колесами, предназначенный для ступенчатого изменения передаточного отношения расчетной кинематической цепи. Они применяются в основном в редко перенастраиваемых цепях при большом диапозоне и количестве передаточных отношений органа настройки расчетной цепи. Эти механизмы отличаются простотой конструкции. Основной недостаток гитар – трудоемкость настройки.

В станках используют гитары с одной, двумя и тремя парами сменных зубчатых колес. Гитара с одной парой сменных зубчатых колес (см. рис. 1.2) применяется в основном в цепях, не требующих точной настройки (органы настройки i_v и i_s). Гитары с двумя и тремя парами сменных зубчатых колес используются, как правило, для точной настройки кинематических цепей (органы настройки i_x, i_y и т.п.). На рис. 2.19 показаны гитары с двумя и тремя парами сменных зубчатых колес.

Гитара с двумя парами колес (рис.2.19, а) состоит из плиты 1, оси 2, фиксирующего болта 3 и сменных зубчатых колес a, в, c, d. Поскольку сумма зубьев сцепляемых колес при различных настройках различна, в плите гитары предусмотрен паз, позволяющий перемещать ось 2 и таким образом осуществлять зацепление сменных колес c и d различных диаметров. Болтом 3 фиксируют плиту гитары в требуемом положении для сцепления колес а и в.

Для подбора зубчатых колес пользуются единственным уравнением с четырьмя неизвестными

, (*)

где i – передаточное отношение, полученное по ФН; a, b, c, d - числа зубьев колес гитары.

Число решений уравнения (*) ограничено следующими факторами:

- имеющимся набором сменных зубчатых колес;

- условиями сцепляемости

а + в > с + (15…20) (**); с +d > в + (15…20) (***).

Для подбора сменных зубчатых колес используют в основном два следующих метода: основной и дополнительный.

Рис. 2.19. Гитары сменных зубчатых колес: а – с двумя парами

сменных колес; б – развертка гитары с двумя парами сменных

колес; в - гитара с тремя парами сменных колес

Основной метод – разложение на простые множители. Используется, когда i выражается простой дробью, числитель и знаменатель которой разлагаются на простые множители, удобные для подбора колес. Например,

.

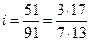Допустим, что в наборе сменных зубчатых колес станка имеются колеса с числами зубьев, кратными пяти от 20 до 100. Тогда,

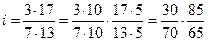
Проверяем условия сцепляемости (**) по допустимому зачению

30 + 70 = 85 + 15.

Возможно, что зубчатое колесо будет перерезать ведомый вал (рис.2.19,б) и, следовательно, монтаж колес невозможен. Поменяем местами колеса в числителе или знаменателе. Например,

.

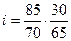Проверяем условия сцепляемости по большему допустимому значению: (**) 85 + 70 > 30 + 20; (***) 30 + 65 > 70 + 20.

Условия сцепляемости подтверждают возможность монтажа подобранных сменных зубчатых колес в гитаре.

Дополнительный метод – приближенный подбор. В этом случае используют способ непрерывных дробей или чаще табличный метод.

Пусть по формуле настройки i = 0, 309329. По таблицам (см., например, М.В. Сандаков и др. Таблицы для подбора шестерен: Справочник. – 6-е изд. М.: 1988. – 571 с.) подбираем соответствующую этой десятичной дроби простую дробь. После преобразований получим числа зубьев сменных колес

.

Такие зубчатые колеса имеются в нормальном наборе сменных зубчатых колес, например, зубофрезерных станков. Проверяем условия сцепляемости: (**) 21 + 65 > 45 + 20; (***) 45 + 47 > 65 + 20.

В ряде станков, например зубофрезерных, как правило, предусматривается более широкий диапозон настройки кинематических. Поэтому в таких станках используются гитары с тремя парами сменных зубчатых колес. В этих гитарах (рис.2. 19, в) используется дополнительная пара зубчатых колес, а в ее плите выполняется два или три паза для промежуточных осей. Для подбора зубчатых колес используется уравнение с шестью неизвестными

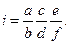
Зубчатые колес e и f меняются значительно реже, чем колеса а,в,с,d. Как правило их передаточное отношение постоянно и равно 1; 1/2; 2. Это позволяет для данной пары колес использовать только четыре сменных зубчатых колеса, например с числами зубьев 40, 60, 60, 80.

Колеса а, в, с, d подбираются по правилам подбора колес для двухпарной гитары, а к условиям сцепляемости добавляется еще одно

e + f > d + (15…20)

Для различных групп станков комплекты сменных зубчатых колес различны. Однако все комплекты создаются на основе общего ряда чисел зубьев сменных колес: 20 – 23 - 25 – 30 – 33 – 34 – 37 – 40 - 41 – 43 – 45 – 47 – 50 – 53 – 55 – 58 – 59 – 60 – 62 – 65 – 67 – 70 – 71 – 73 -75 – 79 – 80 - 83 – 85 – 89 – 90 – 92 – 95 – 97 – 98 – 100 – 105 – 113 – 115 – 120 – 127 - всего 44 колеса.

Для токарно-винторезных станков принят набор колес, у которых числа зубьев кратны пяти (в комплекте 22 колеса).

Набор зубчатых колес для зуборезных станков ограничен колесом с числом зубьев 100. В затыловочных станках набор колес аналогичен общему, но в нем нет колеса со 113 зубьями. Для фрезерных станков (для настройки делительных головок) набор состоит из колес с числами зубьев: 25 – 25 – 30 – 35 – 40 – 50 – 55 – 60 – 70 – 80 – 90 – 100 (всего 12 колес).

Дата добавления: 2015-04-24