
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Планетарные дифференциалы
|
|
|
|
С цилиндрическими колесами. Находящиеся в зацеплении между собой колеса с числами зубьев  и
и  ,
,  связанные ручагом – водилом В представляют собой дифференциал с цилиндрическими зубчатыми колесами (рис.2.22). При сообщении ведущим звеньям колесу
связанные ручагом – водилом В представляют собой дифференциал с цилиндрическими зубчатыми колесами (рис.2.22). При сообщении ведущим звеньям колесу 
 и водилу В соответственно вращательных движений
и водилу В соответственно вращательных движений 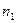 и
и  на ведомом звене – колесе
на ведомом звене – колесе 
 произойдет алгебраическое сложение этих движений с учетом передаточного отношения механизма. Связь между угловыми скоростями приводных звеньев дифференциалаустанавливается по формуле Виллиса (ФВ)
произойдет алгебраическое сложение этих движений с учетом передаточного отношения механизма. Связь между угловыми скоростями приводных звеньев дифференциалаустанавливается по формуле Виллиса (ФВ)
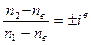 ,
,
где 
 - соответственно круговые частоты (угловые скорости) приводных звеньев;
- соответственно круговые частоты (угловые скорости) приводных звеньев;  - передаточное отношение механизма при остановленном водиле. Знак (+) принимается при одноименном направлении вращения ведущего и ведомого звеньев, а знак (−) - при разноименном направлении их вращения.
- передаточное отношение механизма при остановленном водиле. Знак (+) принимается при одноименном направлении вращения ведущего и ведомого звеньев, а знак (−) - при разноименном направлении их вращения.
Решая ФВ относительно ведомого звена, после несложных преобразований получим
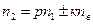 ,
,
где 


При 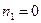 ,
, 
 ; при
; при  ,
, 

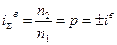 ,
,
где 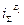 ;
;  передаточное отношение суммирующего механизма при одном остановленном звене соответственно ведущем колесе или водиле.
передаточное отношение суммирующего механизма при одном остановленном звене соответственно ведущем колесе или водиле. 
При расчете настройки кинематических цепей необходимо выяснить назначение дифференциала и установить каким его подвижным звеньям сообщаются круговые частоты  . Рассмотрим в качестве примера привод вращения шпинделя токарно-затыловочного станка модели 1708.
. Рассмотрим в качестве примера привод вращения шпинделя токарно-затыловочного станка модели 1708.

Рис.2.23. Планетарный дифферециал в приводе вращения шпинделя
В этом приводе (рис. 2.23) используется два электродвигателя М1 и М2,
кинематически связанных с входными звеньями дифференциала соответственно водилом В и колесом с внутренним зубчатым венцом Z80.
Выходное звено дифференциала – колесо Z40. Таким образом,
n1 = nZ80; n2 = nZ40; nв = nZ24.
По ФВ получим
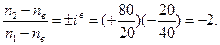
Откуда,
n2 = - 2n1 + 3nв.
Определим передаточные отношения дифференциала при отключенных по очереди электродвигателях.
Электродвигатель М1 отключен. Тогда,
пв=0; n2=-2n1; 
 .
.
Электродвигатель М2 отключен. Тогда,
n1=0; n2=3nв; 
Определим посредством УКЦ возможные круговые частоты вращения шпинделя.
Электродвигатель М1 отключен. Тогда,
nш=(nМ1=1430) ∙ 160/130 ∙ 1/24 ∙ ( ∙22/88 ∙ 20/120 =6 мин-1.
∙22/88 ∙ 20/120 =6 мин-1.
Электродвигатель М2 отключен.Тогда,
nш=(nM2=1430) ∙ 190/140 ∙ 1/24 ∙ (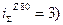 ∙ 22/88 ∙ 20/160 =10 мин-1.
∙ 22/88 ∙ 20/160 =10 мин-1.
Оба электродвигателя вращаются одновременно в одну сторону. Тогда на выходном звене дифференциала круговые частоты складываются. Следовательно, пш=16 мин-1.
Оба электродвигателя вращаются одновременно в противоположные стороны. Тогда на выходном звене дифференциала круговые частоты вычитаются. Следовательно, пш=4 мин-1. 
В рассмотренной схеме дифференциал обеспечивает расширение диапозона настройки круговых частот вращения шпинделя.
С коническими колесами. На рис 2.24 представлена схема планетарного дифференциала с такими колесами. При сообщении ведущим звеньям дифференциала (рис. 2. 24, а), например, водилу В и зубчатому колесу Z2 вращательных движений соответственно пв (или 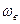 ) и п2
) и п2  на ведомом звене – колесе Z1 произойдет алгебраическое сложение этих движений. Связь между круговыми частотами (или угловыми скоростями) в таком дифференциале устанавливается также по ФВ. Однако в данном случае осуществим определение передаточных отношений дифференциала иным путем.
на ведомом звене – колесе Z1 произойдет алгебраическое сложение этих движений. Связь между круговыми частотами (или угловыми скоростями) в таком дифференциале устанавливается также по ФВ. Однако в данном случае осуществим определение передаточных отношений дифференциала иным путем.
При  вращение сателлитов можно рассматривать (2.24,б) как вращение относительно мгновенного центра вращения М. Тогда,
вращение сателлитов можно рассматривать (2.24,б) как вращение относительно мгновенного центра вращения М. Тогда,
v1=  r1;
r1; 


Следовательно,

 (или
(или 
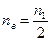 ).
).
Аналогично при  , получим
, получим
 (или
(или  ).
).
Если  и
и 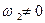 , то
, то
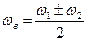 (или
(или  ).
).
Определим передаточные отношения дифференциала при одном останавливаемом звене.
Водило ведущее, п2=0. Тогда,
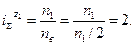
Водило ведомое, п2=0. Тогда,

Ведущее колесо Z1 или Z2, пв=0. Тогда, 
Сравнивая планетарные дифференциалы, отметим следующую особенность при определении передаточных отношений:
- передаточные отношения дифференциала с цилиндрическими колесами зависят от чисел зубьев колес, используемых в дифференциале;
- передаточные отношения дифференциала с коническими колесами от чисел зубьев используемых колес не зависят и, следовательно, имеют постоянное значение.

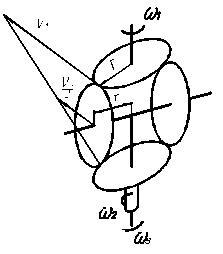
а б
Рис. 2.24. Дифференциал с коническими колесами
В современных металлорежущих станках используются оба типа планетарных дифференциалов. Выбор схемы планетарного дифференциала с цилиндрическими или коническими колесами зависит от традиций, сложившихся в соответствующих конструкторских бюро.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1549; Нарушение авторских прав?; Мы поможем в написании вашей работы!