
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод потенциалов
|
|
|
|
Для получения оптимального плана методом потенциалов рассмотрим следующий исходный план перевозок (табл. 2.6).
Таблица 2.6
| Поставщики | Потребители | Объемы вывоза, тонн | |||
| М1 | М2 | М3 | М4 | ||
| П1 | |||||
| П2 | |||||
| П3 | |||||
| Объемы завоза, т |
Сущность метода потенциалов состоит в том, что для каждой строки и каждого столбца таблицы (табл. 2.7) определяют специальные числа, называемые потенциалами. С помощью этих потенциалов можно установить, нужно ли заполнять свободную клетку матрицы или ее нужно оставить незаполненной.
Таблица 2.7
| Поставщики и объемы вывоза, т | Потребители и объемы завоза | ||||||||||||||||
| М1 | М2 | М3 | М4 | ||||||||||||||
| Потенциалы строк | |||||||||||||||||
| П1 | |||||||||||||||||
| П2 | |||||||||||||||||
| П3 | |||||||||||||||||
| Потенциалы столбцов | |||||||||||||||||
Потенциалы строк и столбцов определяются по заполненным клеткам, находящимся на их пересечении.
Элемент заполненной клетки должен равняться сумме потенциалов строки и столбца, на пересечении которых находится эта заполненная клетка.
Для начала вычислений первый потенциал для строки или столбца принимается условно равным нулю, все остальные потенциалы определяются с помощью элементов заполненных клеток.
Обозначив потенциалы строк ui, потенциалы столбцов Vj, элементы заполнения клеток  , можно записать порядок расчета потенциалов для общего случая.
, можно записать порядок расчета потенциалов для общего случая.
Из основного требования  = ui + Vj вытекает:
= ui + Vj вытекает:
ui =  - Vj; Vj =
- Vj; Vj =  - ui
- ui
Из этих выражений видно, что для расчета потенциала строки необходимо иметь заполненную клетку, в столбце которой потенциал уже определен, а для расчета потенциала столбца нужна заполненная клетка, имеющая потенциал в строке.
В таблице для строки П1 условно принимаем потенциал, равный 0. Эта строка имеет две заполненные клетки, по которым можно определить потенциалы двух столбцов М1 и М2:
для М1 V1 = 18 – 0 = 18;
для М2 V2 = 15 – 0 = 15.
Имея потенциал столбца М2, можно рассчитать потенциал строки П2 по заполненной клетке П2 М2. Потенциал для П2 будет равен:
u2 = 21 – 15 = 6.
По клеткам П2М3 и П2М4 определяются потенциалы столбцов М3, М4. Они будут равны соответственно:
V3 =  - u2 = 12 – 6 = 6;
- u2 = 12 – 6 = 6;
V4 = 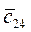 - u2 = 15 – 6 = 9.
- u2 = 15 – 6 = 9.
Для строки П3 - потенциал определяется по метке П3М4.
Он равен:
u3 =  - V4 = 27 – 9 = 18
- V4 = 27 – 9 = 18
Потенциалы показаны в таблице 2.7.
После того, как по строкам и столбцам определены потенциалы, с их помощью выясняется, является ли план оптимальным, и если нет, то, как его можно улучшить. С этой целью для каждой свободной клетки вычисляется сумма потенциалов строк и столбцов, на пересечении которых находится эта клетка.
Сравнение суммы потенциалов с величиной элемента в свободных клетках позволяет определить, нужно ли заполнять эту клетку или ее нужно оставить свободной.
При решении задач на минимум функционала (в нашем случае на минимум тонно-километровой работы) не заполняются те свободные клетки, в которых сумма потенциалов меньше величины элемента (в нашем случае - расстояния). А при решении задач на максимум функционала свободными оставляются те клетки, в которых сумма потенциалов больше величины элемента.
Иными словами, если характеристика, значение которой равно разности  - (ui + Vj), положительная, то свободная метка не заполняется при решении задачи на минимум функции. И наоборот, если она отрицательная, то клетка не заполняется при решении задачи на максимум функции.
- (ui + Vj), положительная, то свободная метка не заполняется при решении задачи на минимум функции. И наоборот, если она отрицательная, то клетка не заполняется при решении задачи на максимум функции.
Свободные клетки, имеющие нулевое значение характеристики, показывают на то, что их заполнение приведет к перераспределению поставок, но объем работ (значение функционала) останется неизменным.
Суммы потенциалов, значения элементов и характеристики для незаполненных клеток приведены в таблице 2.8.
Таблица 2.8
| Шифры клеток | П1–М3 | П1–М4 | П2–М1 | П3–М1 | П3–М2 | П3–М3 |
| Суммы потенциалов | ||||||
| Значение элементов | ||||||
| Характеристики | +1 | +12 | -6 | -15 |
В первоначальном плане две клетки имеют положительные характеристики, в двух клетках характеристики равны нулю (суммы потенциалов равны значениям элементов) и в двух клетках характеристики отрицательные.
Так как задача решается на минимум целевой функции, то именно эти две последние клетки должны быть заполнены поставщиками. Но заполнение свободной клетки и связанное с ним перераспределение поставок производится не изолированно, а в связи с несколькими заполненными клетками. Эта связь выявляется путем построения замкнутых многоугольников, вершинами которых являются клетки таблицы. Одна вершина многоугольника находится в свободной клетке, а все остальные - в заполненных клетках. Многоугольник, или как его называют цепь, имеет прямые углы и четное число вершин.
В результате перераспределения в каждой вершине (клетке) цепи происходит изменение величины поставок: в одних клетках они увеличиваются, в других - уменьшаются.
 |
Те клетки цепи, у которых поставки увеличиваются, называются положительными, а те, у которых поставки уменьшаются - отрицательными. Каждая цепь имеет одинаковое число положительных и отрицательных вершин (клеток). Положительные и отрицательные вершины чередуются. Если свободную клетку, в которую предполагается произвести запись, принять как положительную (поскольку изменение произойдет в сторону увеличения), то следующая клетка будет отрицательной, затем опять положительной, снова отрицательной, и т.д. Для свободных клеток, имеющих отрицательные характеристики, цепи показаны ниже.
Из свободных клеток для заполнения выбирают обычно клетку, которая имеет наибольшую отрицательную характеристику. В нее записывают самую наименьшую величину из отрицательных вершин цепи.
В нашем примере запись поставки, равной 9, произведена в клетке П3-М2 и перераспределение, вызванное этой записью, показано в следующей таблице (табл. 2.9).
Таблица 2.9
| Поставщики и объемы вывоза, т | Потребители и объемы завоза | ||||||||||||||
| М1 | М2 | М3 | М4 | ||||||||||||
| Потенциалы строк | |||||||||||||||
| П1 | |||||||||||||||
| П2 | |||||||||||||||
| П3 | |||||||||||||||
| Потенциалы столбцов | |||||||||||||||
Объем работ составит:
27 * 18 + 9 * 15 + 9 * 21 + 27 * 12 + 27 * 15 + 9 * 18 = 1701 ткм.
Характеристики свободных клеток последнего плана равны:
| Шифры клеток | П1–М3 | П1–М4 | П2–М1 | П3–М1 | П3–М3 | П3–М4 |
| Характеристики | +12 | +12 | +9 | +15 | +15 |
Все свободные клетки имеют положительные характеристики, которые свидетельствуют о том, что дальнейшее улучшение плана невозможно и полученный план является оптимальным. Таким образом, для оптимального плана перевозок транспортная работа составила 1701 ткм.
Для решения задач методом потенциалов исходный план должен иметь количество заполненных клеток m + n – 1 (m - число строк, n - число столбцов). Если план не отвечает этим требованиям, то не для всех строк и столбцов можно рассчитать потенциалы, а без них нельзя проверить план на оптимальность.
Случаи, когда в плане число заполненных клеток меньше m + n – 1, называются вырождением. Вырождение в задаче устраняется путем заполнения недостающих до m + n – 1 клеток нулевыми поставками. Выбор клеток для записей нулевых поставок производится с таким расчетом, чтобы все m + n – 1 заполненные клетки могли быть вычеркнуты, если последовательно производить вычеркивание заполненных клеток единственных в своем столбце или в своей строке.
Если в транспортных задачах не сбалансируются итоги (объемы вывоза превышают объемы завоза или объемы вывоза ниже объемов завоза), то для баланса вводятся дополнительные поставщики или потребители.
Когда объемы вывоза превышают объемы завоза, то вводятся дополнительный столбец, в котором отражается избыток вывоза. Когда объемы завоза превышают объемы вывоза, то вводится дополнительная строка, в которой отражается недостающая часть вывоза. В дополнительных столбцах и строках значения элементов принимаются нулевые.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1261; Нарушение авторских прав?; Мы поможем в написании вашей работы!