Практическое занятие 1. Модуль 1. Оптимизационные методы и модели

Модуль 1. Оптимизационные методы и модели

Цель: освоить симплекс-метод, приобрести навыки использования информационных систем управления и управленческого учета для решения задач оптимизации

Задача 1 (Ассортиментная задача)

Цех кондитерской фабрики вырабатывает три ассортиментные группы конфет, условно обозначенные M₁, М₂, М3 /в ед./.

Для их производства используются основные виды ресурсов /сырья/ трех видов, условно названных П₁, П₂, П₃ /в ед./.

Расход каждого ресурса на производство единицы продукции является заданной величиной, определяется по рецептуре и обозначается символами а₁₁, a₁₂..., а₃₃, где а - норма расхода, первая подстрочная 1 - номер ресурса, вторая подстрочная 1, 2, 3 - номер ассортиментной группы кон­фет.

Наличие каждого ресурса для производства всех, групп конфет прини­мается как известная величина и обозначается символами в₁, в₂, в₃.

Прибыль на продукцию также принимается как известная величина и обозначается символами с₁, с₂, с₃.

Перечисленные параметры являются величинами известными и выражают­ся в единых единицах измерения, кроме прибыли. Прибыль или другой ка­кой показатель, являющийся критерием оптимальности, выражается в еди­ницах измерения дохода /например, прибыли/, получаемого от производства единицы продукции в денежном или другом каком-нибудь выражении.

Поскольку решение задачи заключается в поиске такого плана производ­ства, который обеспечивал бы в принятых условиях наибольший доход, при­нимаются те величины, которые являются неизвестными и обозначающими количества каждой группы конфет, включаемых в план производства: х₁ для M₁; х₂ для М₂; х₃ для М₃.

Экономико-математическая модель в символическом виде.

Система ограничений

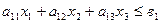
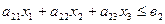
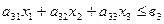
Целевая функция /суммарный доход/ F = 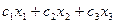= мах

Условия неотрицательности неизвестных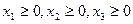

Символическая модель, наполненная численной информацией, будет иметь следующий вид:

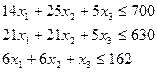
Прибыль от реализации выпускаемой продукции должна быть максимальной, то есть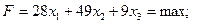

Решение задачи.

Для решения задачи симплексным методом неравенства преобра­зуются в эквивалентные равенства путем добавления в каждое нера­венство по одному дополнительному неизвестному с коэффициентом + 1 и нулевым уравнением прибыли. Для удобства расчетов левые и правые части уравнений меняются местами. В этом случае исходные неравенства примут вид симплексных уравнений:

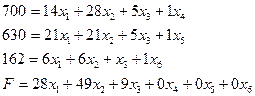
Коэффициенты пря неизвестных записываются в симплексной таблице, в которой выполняются расчеты и отражаются полученные результаты.

Исходная таблица.

сj	p0	x0
x1	x2	x3	x4	x5	x6
	x4
	x5
	x6
Zj - Cj		-28	-49	-9

В столбцах таблицы записывают: в первом (С_j) - прибыль единицы продукции, которая вводится в план выпуска; во втором (Р₀) – неизвестные, включаемые в план; в третьем (Х₀) - – свободные величины; в остальных - коэффициенты при неизвестных уравнений. В верхней части этих столбцов отражаются коэффициенты при неизвестных целевой функции.

В нижней строке (целевой) записываются получаемые расчетным путем показатели: в столбце х₀ - суммарная прибыль планового выпуска, в остальных столбцах - прибыль единицы продукции с отрицательным знаком.

В последних трех столбцах коэффициенты при дополнительных неизвестных, равные единице, расположены по диагонали. Эта часть таблицы, называемая единичной подматрицей, необходима для вычислительных и аналитических целей.

При решении задач на максимум целевой функции наличие в целевой строке отрицательных чисел указывает на возможность начала или продолжения решения задачи. Порядок решения таков: из отрицательных чисел целевой строки выбирается наибольшее по модулю. Столбец, в котором оно находится, принимается за ключевой (или разрешающий) и для удобства расчетов выделяется. В нашем примере таким столбцом будет х₀, имеющий в целевой строке наибольшую по модулю величину - 49.

1-ая итерация

сj	p1	x0	x1	x2	x3	x4	x5	x6
	x2		1/2		5/28	1/25
	x5		21/2		5/4	-3/4
	x6				-1/14	-3/14
Zj - Cj		-7/2		-1/4	7/4

Затем элементы столбца x₀ (свободные величины) делят на соответствующие коэффициенты ключевого столбца и полученные результаты сопоставляют между собой. Строка с наименьшим отно­шением принимается за ключевую и также для удобства выделяется. В нашем случае 700/I4 = 25, 630/21= 30, 162/6 = 27. Наимень­шее отношение 25 имеет срока х₄, она и будет ключевой. Ключевой элемент 28.

Далее элементы таблицы преобразуются и записываются в новую таблицу. Первоначально преобразуют элементы ключевой строки путем деления их на ключевой элемент. Преобразованные элементы записывают в том же самом месте.

В столбцах Р₀ и С_j занимают место вводимая в план неиз­вестная x₂ с прибылью 49 (итерация 1-я). Остальные элемен­ты преобразуются по следующему правилу:

- для преобразуемого элемента в его столбце находят элемент ключевой строки, а в его строке - элемент ключевого столб­ца;

- соответствующие элементы ключевой строки и ключевого столбца перемножаются и полученное произведение делят на ключе­вой момент;

- частное от деления вычитают из значения элемента, кото­рое он имел до преобразования, и полученный результат будет преобразованным элементом, который записывается в новую таблицу в том же самом месте.

Следуя этому правилу, преобразование элементов столбца х₀ будет:

630 -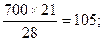

162 -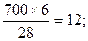

0 -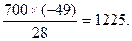

Включение на первой итерации в план неизвестной х₂ (выпуска продукции П вида) обеспечит сумму прибыли 1225 руб.

Решение задачи продолжается, так как в целевой строке два отрицательных элемента. Наибольший по модулю элемент - 7/2. Он находится в столбце х₁, который принимается за ключевой, а ключевой строкой будет х₆ (25:1/2=50; 105:21/2=10; 12:3=4). Элементы таблицы преобразуются в том же порядке по изложенному правилу и записываются в новую таблицу.

2-я итерация

сj	p2	x0	x1	x2	x3	x4	x5	x6
	x2				4/21	1/14		-1/6
	x5				3/2			-7/2
	x1				-1/42	-1/14		1/3
Zj - Cj				-1/3	3/2		7/6

В полученном на 2-й итерации плане ключевым столбцом будет х₃, ключевой строкой х₅ (23:4/21=121; 63:3/2=42, при отрицательном элементе отношение не определяется), ключевым элементом 3/2. Элементы ключевой строки преобразуются деле­нием их на ключевой элемент. Остальные элементы преобразуются рассмотренным выше или более упрощенным способом, смысл которого заключается в следующем:

- для преобразуемого элемента в его столбце уже преобразованный элемент ключевой строки (в новой таблице), а в его строке - еще не преобразованный элемент ключевого столбца (в предыдущей таблице);

- найденные элементы перемножаются и полученный результат вычитается из значения элемента, которое он имел до преобразо­вания.

3-я итерация

сj	p2	x0	x1	x2	x3	x4	x5	x6
	x2					1/14	-8/23	5/18
	x5						2/3	-7/3
	x1					-1/14	1/63	5/18
Zj - Cj					3/2	2/9	7/18

Этот новый результат является преобразованным элементом и записывается в новой таблице в том же самом месте. По этому правилу преобразуем элементы столбца х₆. Дня элемента -1/6 в его столбце уже преобразованный элемент ключевой строки в новой таблице -7/3. Этот элемент умножается на еще не преобразованный элемент ключевого столбца 4/21. Полученный результат вычитается из преобразуемого элемента и записывается в новой таблице:

-1/6 - (-7/3 * 4/21) = 5/18

Так же и для двух других элементов:

1/3 – [(-7/3) - (-1/42)] = 5/18; 7/6 – [(-7/3) * (-1/3)] = 7/18

Остальные элементы преобразованы в таком же порядке и записаны в таблицу 3.

В последней таблице целевая строка имеет только положительные элементы. Это значит, что составленный план оптимален и дальнейшее улучшение его невозможно.

Как видно из таблицы, оптимальный план предусматривает выпуск продукции П₁ 5 ед. (х₁ = 5), П₂ вида 15 ед. (х₂ = 15), П₁ вида 42 ед. (х₃ = 42). Дополнительные неизвестные в план не вошли, следовательно, х₄ = 0, х₅ = 0, х₆= 0. Подставив значе­ния неизвестных в уравнения, получим:

14*5 + 28*15 + 5*42 + 0 = 700

21*5 + 21*15 + 6*42 + 0 = 630

6*6+ 6*15 + 1*42 + 0 = 162

F = 28*5 + 49*15 + 9*42 = 1253

При постановке задачи были приняты ограничения только по запасам сырья. Другие ограничения не учитывались. Но если бы в плане требовалось предусмотреть ассортиментные соотношения (например, выпуск продукции I вида должен быть не меньше выпуска продукции II вида, т.е. х₁ 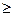х₂), то в систему неравенстве добавляется это ограничение:

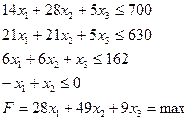
Эта система преобразуется в симплексные уравнения и ре­шается по изложенным правилам.

Проведем анализ оптимального плана.

а) Запасы сырья трех видов используются полностью без остатка, так как х₄ = х₅ = х₆ = 0.

б) Рассмотрим элементы матрицы.

Элементы столбца х₁ свидетельствуют: если запасы муки будут увеличены на I ед. (х₄ = 1), то выпуск продукции II вида увели­чится на 1/14 ед. (х₄ = 15 + 1/14), выпуск продукции III вида не изменится, выпуск продукции I вида уменьшится на 1/14 ед. (5 - 1/14). Сумма прибыли увеличится на 1,5 руб.

Элементы столбца х₅ показывают, что увеличение запасов сахара на I ед. (х₅ = I) позволит увеличить выпуск продукции III вида на 2/3 ед., I вида на 1/63 ед., прибыль на 2/9 руб. и снизить выпуск продукции II вида на 8/23 ед. Изменения объемов производства и суммы прибыли вызовет и увеличение запасов жира (см.столбец х₆). Снижение запасов сырья приводит к изменениям выпуска продукции и суммы прибыли в обратном порядке.

Элементы целевой строки оптимального плана называются двойственными сценками, которые определяют величину изменения прибыли при изменении запасов сырья на I ед.

Дата добавления: 2015-04-24