Пример 4.1. Применение метода наименьших квадратов

Применение метода наименьших квадратов

Практическое занятие 4

Модели управления

Модуль 2. Сетевое планирование и другие

Цель: закрепление теоретических знаний, овладение навыками сравнения различных прогнозирующих трендов и проведение расчетов ошибки прогноза.

Представив в графическом виде данные, можно с помощью метода наименьших квадратов подобрать линию, в наибольшей степени соответствующую полученным данным и определить прогнозную величину исследуемого признака.

Рассмотрим метод наименьших квадратов, который находит применение в прогнозах с использованием статистического моделирования.

Для линейного тренда

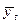= a+bt

система нормальных уравнений:

ìS y_t=na + b S t,

í (4.1)

îS y_tt =a S t + b S t²

Подставив в систему (4.1) имеющуюся исходную информацию (y_t и t) можно рассчитать параметры прогнозирующей функции, а и b. Сомножитель n - длина временного ряда.

В таблице 4.1 представлен объем продаж онкологических препаратов на оптовой фирме (тыс. руб.) за 14 месяцев. Провести расчет параметров линейного тренда и сделать прогноз на 15, 16 и 17 месяцы.

Построить графики ряда динамики и тренда.

Таблица 4.1

Месяцы, t	объем продаж онкологических препаратов (тыс. руб.), yt	ytt	Линейный тренд
		145,000	246,967
		628,000	294,960
		1290,000	342,953
		2100,000	390,946
		1735,000	438,939
		1770,000	486,932
		2982,000	534,925
		4824,000	582,918
		4932,000	630,911
		5980,000	678,904
		7315,000	726,897
		9696,000	774,890
		11674,000	822,883
		11550,000	870,876
Итого		66621,000	7824,901

Для определения численных значений констант уравнения (4.1) удобно пользоваться таблицей 4.1.

Необходимо посчитать все суммы:

S t = 105, S t² = 1015, S y_t = 7427, S y_t t = 66621,

и подставить их в систему нормальных уравнений:

7427,0 = 14× a + b ×105

66621,0 = a ×105 + b ×1015

найдем свободный член уравнения a =198,974 и коэффициент пропорциональности b = 47,993. Таким образом, прогнозная модель имеет вид

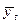= 198,974 + 47,993 × t

Подставляя значения t=1,2…14, получим значения линейного тренда (табл.4.1). После того как мы получили линейный тренд, можно прогнозировать развитие процесса в будущем. Для этого надо подставить в полученную формулу значения t = 15, 16, 17.

Расчеты выполним по формулам:

y_t=15 = 198,974 + 47,993 × 15 = 918,869 тыс. руб.

y_t=16 = 198,974 + 47,993× 16 = 966,862 тыс. руб.

y_t=17 = 198,974 + 47,993× 17 = 1014,855 тыс. руб.

Нанесем полученные данные на график (рис. 4.1).

Рис. 4.1 Построение линейного тренда к исходному ряду

Из графика видно, что изменение выпуска продукции можно приблизить линейной зависимостью.

Дата добавления: 2015-04-24