II итерация

I итерация

Сj	P0	X0
X1	X2	X3	X4	X5	X6
	X4		5/4	11/4				-1/4
	X5		7/4	5/4				-3/4
	X6		3/4	1/4				1/4
F		-3	-13

Затем элементы столбца X₀ (свободные величины) делят на соответствующие коэффициенты ключевого столбца и полученные результаты сопоставляют между собой. Строка с наименьшим отношением принимается за ключевую и также для удобства выделяется. В нашем случае

Наименьшее отношение 50 имеет строка X₄. Она и будет ключевой. Ключевой элемент 28.

Далее элементы таблицы преобразуются и записываются в новую таблицу. Первоначально преобразуют элементы ключевой строки путём деления их на ключевой элемент. Преобразованные элементы записывают на том же самом месте.

В столбцах P₀ и C_j занимают место вводимая в план неизвестная x ₁ с прибылью 28.

Остальные элементы преобразуются по следующему правилу:

§ для преобразуемого элемента в его столбце находят элемент ключевой строки, а в его строке – элемент ключевого столбца;

§ соответствующие элементы ключевой строки и ключевого столбца перемножаются и полученное произведение делят на ключевой элемент;

§ частное от деления вычитают из значения элемента, которое он имел до преобразования. Полученный результат будет преобразованным элементом, который записывается в новую таблицу в том же самом месте.

Следуя этому правилу, преобразование элементов столбцов будет:

Включение на первой итерации в план неизвестной x ₁ (выпуска продукции П вида) обеспечит сумму прибыли 1400 рублей.

Решение задачи продолжается, так как в целевой строке два отрицательных элемента. Наибольший по модулю элемент (-13). Он находится в столбце X₃, который принимается за разрешающий, а ключевой строкой будет X₄.

Элементы таблицы преобразуются в том же порядке по изложенному правилу П записываются в новую таблицу.

Сj	P0	X0
X1	X2	X3	X4	X5	X6
	X2		5/11			4/11		-1/11
	X5		13/11			-5/11		-7/11
	X3		7/11			-1/11		3/11
F		32/11			52/11		64/11

Задача 2 (Транспортная задача)

Составить оптимальный план перевозок пищевых продуктов от 4-х поставщиков к 6-ти потребителям. Поставщики (П), потребители (М), объемы вывоза и завоза, кратчайшие расстояния между пунктами вывоза и завоза приведены в таблицах.

Поставщики	Потребители	Объемы вывоза, тонн
М1	М2	М3	М4	М5	М6
П1
П2
П3
П4
Объемы завоза, т

При решении транспортных задач ограничениями служат: объемы вывоза (запасы) каждым поставщиком и объемы за­воза (потребности) каждого потребителя.

Обозначим неизвестную величину перевозимого груза от по­ставщиков к потребителям через x с подстрочными индексами.

Индексы показывают координаты каждой неизвестной, т. е. но­мер строки и номер столбца таблицы, на пересечении которых находится данная неизвестная.

В табл. 1.2 представлены принятые объемы вывоза каждым поставщиком, потребности каждого потребителя и неизвестные, которые должны показывать величину перевози­мого груза от поставщиков к потребителям.

Таблица 1.2

Поставщик		Потребитель	Объемы вывоза, т
М1	М2	М3	М4	М5	М6
П1	Х11	Х12	Х13	Х14	Х15	Х16
П2	Х21	Х22	Х23	Х24	Х25	Х26
П3	Х31	Х32	Х33	Х34	Х35	Х36
П4	Х41	Х42	Х43	Х44	Х45	Х46
Объемы завоза, т

Из данных табл. 1.2 можно заключить, что объемы запасов у каждого поставщика должны быть равны сумме переменных, находящихся в строке каждого поставщика. В математической форме это будет выражаться так:

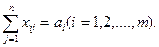(1.1)

Аналогично сумма переменных в каждом столбце должна равняться потребностям соответствующих потребителей:

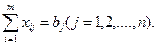(1.2)

Используя переменные, которые показывают величину по­ставляемого потребителям груза и расстояния между постав­щиками и потребителями (см. табл. 1.1), в математической форме можно выразить тонно-километровую работу по перевозке:

При этом считается, что все неизвестные, содержащиеся в уравнениях (1.1), (1.2), (1.3), могут быть выражены только положительными или нулевыми числами. Неизвестные не мо­гут выражаться отрицательными числами, так как это озна­чало бы отрицательную перевозку — от потребителя к по­ставщику. Это математическое условие выражается в форме следующих неравенств:

(1.4)

Следовательно, задача состоит в определении таких значе­ний неизвестных, удовлетворяющих равенствам (1.1), (1.2) и неравенствам (1.4), при которых объем транспортной работы, выраженный равенством (1.3), становится минимальным.

Итак, условия задачи по распределению запасов трех по­ставщиков между пятью потребителями выражены в матема­тической форме, составляющей математическую модель транс­портной задачи линейного программирования.

По изложенной схеме можно составить модель для любого числа предприятий-поставщиков и предприятий-потребителей, выразив ее в математической форме.

В общем виде математическая модель транспортной задачи будет иметь следующее содержание. Необходимо перевести не­которое число единиц однородной продукции от нескольких по­ставщиков к нескольким потребителям. Каждому из этих по­требителей требуется определенная величина продукции и каж­дый поставщик может поставить только определенную величину этой же продукции. Принимаем следующие обозначения: т — число поставщиков; n — число потребителей; а_i — общее коли­чество продукции, выделяемой для перевозки i- мпоставщиком; b_j — общее количество продукции, необходимой j -му потребителю; с_ij — расстояние(или тариф) перевозок продукции от i -гo поставщика до j -го потребителя; x_ij — количество продук­ции, перевозимой от i - гопоставщика к j -му потребителю.

Дата добавления: 2015-04-24