Емкостный фильтр

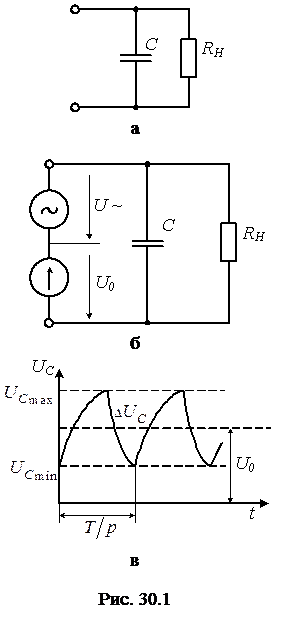Конденсатор С, включенный параллельно нагрузке (рис. 30.1, а), представляет собой простейший емкостный фильтр. При повышении напряжения источника питания конденсатор периодически заряжается и разряжается на нагрузку, когда питающее напряжение становится меньше напряжения на его зажимах. При этом во время разряда конденсатор отдает нагрузке заранее запасенную энергию и напряжение на нагрузке изменяется в относительно меньших пределах, чем при отсутствии конденсатора, в чем и заключается сглаживающее действие емкостного фильтра.

Конденсатор представляет собой емкостное сопротивление для переменного тока, а в данном случае – для переменной составляющей выпрямленного тока, т.е.

(30.2)

где 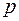– коэффициент, зависящий от схемы выпрямления, ;
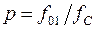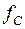– частота питающей сети;
– круговая частота, .

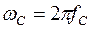Шунтирующее действие конденсатора, включенного параллельно нагрузке, обеспечивает сглаживание пульсаций при выполнении условия

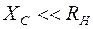, (30.3)

или

. (30.3а)

При соблюдении этого условия большая часть переменной составляющей выпрямленного тока, минуя нагрузку, как бы замкнется через конденсатор.

В общем случае можно считать, что конденсатор фильтра заряжается импульсами тока длительностью, меньшей чем , где 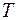– период изменения напряжения сети. Для упрощения расчета фильтра можно предположить, что ток разряда конденсатора неизменен и равен 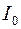– среднему значению тока нагрузки. Изменение напряжения на нагрузке 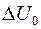можно вычислить как изменение напряжения на конденсаторе 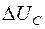при его разряде:

(30.4)

Как видно из рис. 30.1, в, изменение напряжения на конденсаторе представляет собой удвоенную амплитуду переменной составляющей выпрямленного напряжения. Отсюда следует, что выражение, определяющее коэффициент пульсации, 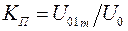с учетом того, что , может быть записано в виде .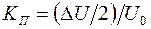

После подстановки в это выражение 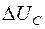из (30.4) и 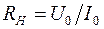получим

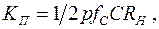(30.5)

откуда ,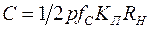
где 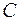– емкость конденсатора, Ф.

Умножив это выражение на 10⁶ и выразив 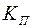в процентах, получим выражение емкости конденсатора С, мкФ:

.

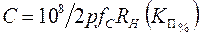Полученные соотношения содержат неточности, обусловленные идеализацией схемы и сделанными выше допущениями. Однако, как показывают опытные данные, погрешности расчета не столь велики, причем при коэффициентах пульсации данные расчетные соотношения обеспечивают достаточную точность и лишь при больших значениях 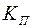точность расчета составляет приблизительно ±10 %.

Получить небольшое значение коэффициента пульсации на нагрузке 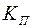при ограниченной емкости конденсатора С можно лишь при большом сопротивлении нагрузки 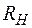, т. е. при небольших выпрямленных токах, вследствие чего емкостный фильтр применяют преимущественно в маломощных выпрямителях.

К преимуществам емкостного фильтра можно отнести простоту его выполнения, к недостаткам – необходимость применения диодов, рассчитанных на большую амплитуду прямого тока .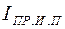

Дата добавления: 2015-04-24