Основные цели и задачи динамических расчетов, механических систем с учетом упругости звеньев. 2 страница

13. КРУТИЛЬНЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ.

Крутильный маятник – упругий безинерционный вал диаметром d, длиной l.

Абсолютно жесткий диск диаметром D, с моментом инерции I.

Если диск повернуть на малый угол φ относительно оси вала и отпустить, то крутящий момент, появившийся при закручивании вала, приведет его в состояние свободных крутильных колебаний. При этом момент, передаваемый на диск от закрученного вала, пропорционален углу закручивания и всегда действует противоположно вращению диска:

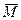= -с_к · , где с_{к –} жесткость при кручении, крутящий момент, отнесенный к единице угла поворота, тогда диф. ур-е движения (гармонические крутильные колебания) запишется: I _φ = - с_к · φ, (9)

где I – момент инерции диска,

φ – угол поворота,

с_к – жесткость при кручении,

– угловое ускорение.

разделим на I 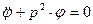(10)

где (11)

Решение уравнение (10) по аналогии с уравнением (4) запишется:

φ = φ_о ·cos pt + · sin pt (12)

в эквивалентном виде

φ = А ·cos(pt-α) (13)

где:

φ_о – угловое перемещение,

– начальная скорость (угловая) в начальный момент времени t=0,

α – фазовый угол;

Период крутильного колебания равен: ;

Частота крутильных колебаний ;

Если вал диаметром d имеет длину l, то жесткость при кручении будет равна:

, (14)

где G - модульупругости II рода (модуль сдвига) [ G для стали = 8,4 · 10¹⁰ Па]

I - момент сопротивления кручению поперечного сечения вала, который в случае круглого сечения равен полярному моменту инерции сечения

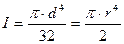
Если диск является однородным и диаметр D и вес известны, то момент инерции диска:

,

где Q – вес,

D – диаметр,

т.е. рассчитав I диска и С_к вала, мы определим р.

Если вал имеет два участка различных диаметров и длин, то требуется определить с_к эквивалентного вала, можно двумя способами:

1 способ. Строится модель с последовательно соединенными пружинами, имеющими разную с_к.

При последовательном соединении безинерционных упругих связей складываются податливости.

Следовательно:

е_экв = е₁ + е₂ =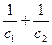

Тогда: с_экв = (15)

2 способ. φ – полный угол закручивания ступенчатоговала будет равен:

φ = + = = ;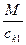

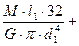
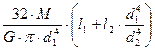таким образом, эквивалентная длина вала диаметром d₁ равна:

L_экв = 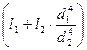(16)

Т.е. угол закручивания вала ступенчатого с двумя диаметрами d₁ и d₂ равен углу закручивания вала с постоянным диаметром d₁ и приведенной длиной L_экв.

Впервые на проблему необходимости исследований крутильных колебаний при проектировании сложных технических систем указал случай вала, работающего на подшипниках (без учета трения), несущего на концах абсолютно жесткие тела: например, вал с пропеллером на одном конце и ротором турбины на другом (в самолетостроении).

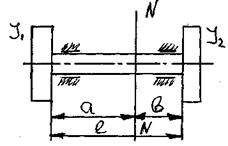
Если 2 диска закрутить в противоположных направлениях, а затем отпустить, возникнут свободные крутильные колебания. Из принципа сохранения момента кол-ва движения следует, что диски всегда должны вращаться в противоположных направлениях, а значит, есть промежуточное поперечное сечение N-N, в котором деформации вала не происходят, так называемое узловое сечение.

Найдем его положение исходя из следующих соображений:

1. Диски должны иметь один и тот же период колебаний, иначе не будет вращения противоположного, т.е.:

2. Т.к. с_к обратно пропорциональна длине, то:

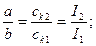
с учетом, что а + в =l, получим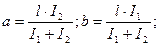

Наличие узлового сечения N-N позволяет перейти к эквивалентной схеме, состоящей из двух крутильных маятников, имеющих одинаковые периоды, частоты собственных колебаний.

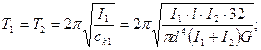
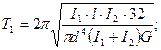
Т.е. если известны размеры вала, моменты инерции вращающихся деталей и модуль упругости материала при сдвиге, то для приводов данной исходной схемы можно определить

р, ν, Т

14. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ЛИНЕЙНЫХ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ БЕЗ ДЕМПФИРОВАНИЯ (установившееся движение).

Если система подвергается внешним воздействиям – силам, зависящим от времени, или специального вида опор, то динамическое поведение её становится более сложным нежели свободное колебание. На практике часто внешние силы изменяются во времени периодически и приложены к массе, в этом случае реакции систем показывают вынужденными колебаниями.

Рассмотрим мех. систему – электродвигатель весом Q закреплен на пружине, которая ограничивает движение системы и та движется только в направлении по оси х. вал электродвигателя вращается с постоянной угловой скоростью ω и имеет дисбаланс D.

1 случай.

D= е·М

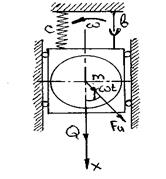F_и = D · ω

cила приложения к массе, D дисбаланс порождает вращающую центробежную силу F_и, которая и вызывает вынужденные колебания системы.

Запишем уравнение движения системы, используя 2-ой закон Ньютона:

m 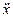= Q – (Q+e x) + F_u sin ω·t

m 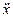+ cx = F_u sin ω·t 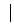: m

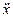+ p²x = q sin ω·t, (17) неоднородное дифференциальное уравнение вынужден-

ных установившихся колебаний

где: q – уд.сила, отнесенная к единице массы.

Частное решение:

х = с₃ sin ω·t подставим в уравнение (17), получим -с₃ ω² sin ω·t + с₃ р² sin ω·t = q sin ω·t

(18)

Общее решение: х = c₁ · cos pt + c₂ · sin pt + 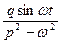, (19)

где: два первых члена описывают свободные колебания системы, которые имеют период Т = ,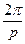

третий член зависит от возмущающей силы, характеризует вынужденное колебание с периодом Т = .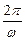

Движение, определяемое уравнением (19), следовательно, представляет сумму 2-х гармонических колебаний, имеющих в общем случае 2 различных периода.

Т.к. в реальной мех. системе действуют силы трения, то свободные колебания со временем затухают и движение приходит к установившимся вынужденным колебаниям, которые полностью описываются уравнением (18)

Вынужденные колебания, поддерживаемые внешней возмущающей силой, имеют большое практическое значение – имеют большое распространенное в технике и окружающем мире.

В уравнение (18) вынесем из знаменателя р ₂: х = ,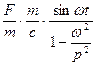

тогда x= , (20) - уравнение установившихся вынужденных колебаний

где: 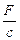·sin ωt – перемещение, обусловленное действием возмущающей силы F sin ωt,

когда она приложена статически;

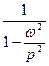– множитель учитывает динамический характер этой силы.

β = 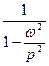, (21) абсолютная величина этого выражения называется коэффициентом

динамичности.

Мы рассмотрели действие силы пропорциональной sin ωt, то же справедливо и дляcos ωt.

2 случай - вынужденных колебаний возможен при периодичеком движении опор

уравнение движения

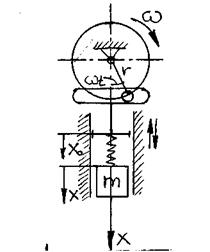
m 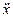= Q – [Q + c(x-x₀)]

x₀ = r· cos ω t

получим:

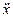+ p²_x = · r ·cos ω t

данное уравнение аналогично выражению (17)

т.е. · r ≡ q, тогда решение данного уравнения запишется: x =

выносим р²

x= r· cos ω t · β (22)

таким образом для того, чтобы вычислить установившееся вынужденное колебание системы достаточно рассмотреть перемещение массы, обусловленное перемещением опоры.

График зависимости β от Z: Z = – коэффициент частотной расстройки

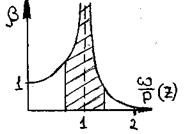
Рассмотрим 3 случая отношения .

1 случай: ω «р значение коэф. β=›1 ( стремится к 1), т.е. перемещение системы близко по значению к случаю статического действия возмущающей силы, кроме того колебания массы и возмущающей силы совпадают по фазе, т.е. перемещение массы совпадает с направлением вектора возмущающей силы.

2 случай: = 0

Амплитуда вынужденных колебаний стремится к ∞, т.е. – условие резонанса (ω=р).

3 случай: ω» р, т.е. β 0 когда на тело действуют с большой частотой, вызываемое колебание имеет очень малую амплитуду, можно говорить, что тело сохраняет стационарное состояние, практически неподвижно. Динамические перемещения в этом случае в противофазе, т.е. масса перемещается в направлении противоположном направлению вектора возмущающей силы.

СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
С УЧЕТОМ ДЕМПФИРОВАНИЯ

Для проведения аналитических исследований при обеспечении более точного результата исследований необходимо учитывать влияние демпфирующих сил:

- трение между сухими поверхностями скольжения;

- трение с учетом смазывающих материалов;

- сопротивление воздуха или жидкостей;

- внутреннего трения материалов.

Простейший случай для математического исследования, когда демпфирующая сила пропорциональна скорости – вязкое демпфирование.

Поэтому силы сопротивления с более сложной природой при исследованиях заменяются силами эквивалентного вязкого демпфирования,

Эквивалентное демпфирование определяют из условия:

за один цикл при нем рассеивается столько же энергии, сколько при действии реальных сил сопротивления.

Рассмотрим расчетную динамическую модель с демпфером.

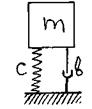
Предположим, что вязкая жидкость в демпфере оказывает сопротивление пропорциональное скорости движения системы.

F = - b , (24)

где: b – коэф.пропорциональности (коэф. вязкого демпфирования),

F – линейная сила сопротивления.

Уравнение движения системы:

m 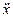= Q –(Q + cx) – b

m 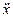+ b + cx = 0 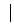: m - дифференциальное уравнение системы свободных

колебаний с демпфированием.

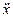+2п + р²х = 0, (25) – дифференциальное однородное уравнение свободных

где: колебаний с демпфированием

2п = 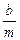– параметр демпфирования.

Решение уравнения (25) в общем виде:

х = е^nt(c₁ · cos p_д t + c₂ · sin p_д t), (26)

где: е - основание натурального логарифма,

п – параметр демпфирования,

р_д – собственная круговая частота с учетом демпфирования.

Рассмотрим начальный момент:

t = 0; x = x₀; = ₀; c₁ = x₀; c₂ = ;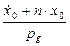

Решение уравнения (25) в эквивалентном виде:

x = A · e^-nt · ( cos p_g ·t – α_g), (27)

где: A = ,

α_g – фазовый угол демпфированной системы, α = arctg

p_g = 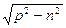; p_g = p 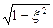, (28) ξ =0,1÷0,2

где: ξ – коэффициент демпфирования системы; ξ = 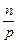; p = p _g.

Возможность использования при решении практических задач вместо p_g значение p, подтвердимграфиком зависимости (ξ)

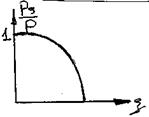
Т.к. практическое значение ξ небольшое, по графику значения ξ соответствуют отношению , очень близко равным к 1.

График свободных колебаний системы с демпфированием:

,

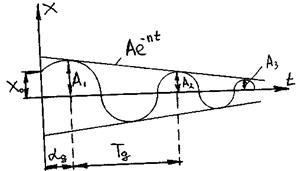
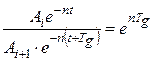где: T_g – период колебаний с демпфированием

n · T_g = λ, (29)

λ – логарифмический декремент затуханий

Для практических задач: λ = n · ≈ ξ ·2 π

Из уравнения (29) λ = ln , (30)

Если при числе колебаний равных k

λ = 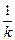· ln (31)

= e^λ (32)

ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ СВОБОДНЫХ КОЛЕБАНИЙ С ДЕМПФИРОВАНЕМ. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА СУХОГО ТРЕНИЯ.

Рассмотрим расчетную динамическую модель, состоящей из жесткости и массы

Выведем из 2-х способов состояние свободного равновесия. Потеря энергии, или совершаемая работа, системы за цикл равна:

ΔW = (cA₁² – cA₂²) = c · (A₁ + A₂) · (A₁ – A₂) = c · A_cp · ΔA

ΔW = 4A_cp ·F_mp

c · A_cp · ΔA = 4A_cp ·F_mp

ΔA = = =

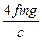f =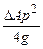

18.

УСТАНОВИВШЕЕСЯ ВЫНУЖДЕННОЕ КОЛЕБАНИЕ С ДЕМПФИРОВАНИЕМ

С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ

В реальных системах кроме сил упругости F = -cx, возникающих в пружине при деформации и силы сопротивления F= -bx часто приводится приложенная извне возмущающая сила, изменяющаяся по гармоническому закону. Например, при работе электродвигателя с неотбалансированным ротором возникает вращающаяся центробежная сила.

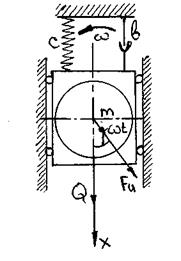
п_оп = (0,7÷1,3) ·п_кр

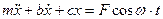/:т

(33) - дифференциальное однородное уравнение вынужденных колебаний с демпфированием

Частное решение:

x = M cos ω t + N sinω t (34)

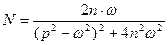
Общее решение: x = e^-nt (c₁ cos p_g ·t + c₂ sin p_g t ) + M cos ω t + N sin ω t

I II

I – описывает демпфированные свободные колебания с периодом T_g = и благодаря множителю e^-nt данное колебание затухает и остаются только установившиеся вынужденные колебания системы, описываемые в слагаемом II, период этих колебаний совпадает с периодом возмущающей силы.

Выражение (34) для установившегося поведения системы может быть записано в эквивалентной форме с фазовым углом

х = A cos(ω ·t –Θ), (35)

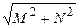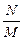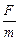где А – амплитуда, A = Θ =arctg q= ξ=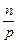

A = 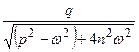= вынесем p² =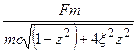

A = 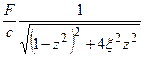(36) -амплитуда вынужденных колебаний с одной степенью

свободы с демпфированием.

β =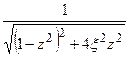

A_g = ·β

x = A_cm· β · cos (ω t- Θ),

где: A_cm = ,

т.е. амплитуда установившихся вынужденных колебаний системы с демпфированием можно получить, умножив величину перемещения системы при статически приложенной нагрузке (А_ст) на коэффициент динамичности β, который в данном случае зависит не только от коэффициента расстройки z = , но и от коэффициента демпфирования ξ, т.е. в выражении β присутствует ξ.

Определим возможно максимальное значение А_дин:

β_max = ; z = = 1;

A_max = · = = ;

A_max = 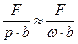(37)
19,20

ОБОБЩЕННАЯ ПЕРИОДИЧЕСКАЯ ВОЗМУЩАЮЩАЯ СИЛА.

Ранее предполагалось, что возмущающая сила вынужденных колебаний описывается функцией пропорциональной либо sin ωt, либо cos ωt. В общем случае встречаются возмущающие силы, описываемые более сложными периодическими функциями.

Пример: Одноцилиндровый двигатель имеет неотбалансированные детали, которые совершают вращательное и возвратно-поступательное движения внутри картера и порождают периодическую возмущающую силу, вызывающую вынужденные колебания всей системы. Требуется установить точный характер возмущающей силы и отношение её периода к периоду собственных колебаний системы.

r – радиус кривошипа

l – длина

ωt – угол поворота

Приведем массы подвижных

частей механизма в т. М ₁ и т. М ₂

F₁ =- М₁ · ω ² · r · cos ωt –

т.к. М ₁ совершает вращательное движение.

(М ₁ и М ₂ – приведенные сосредоточенные массы)

F₂ =- М₂ · х – т.к. М₂ совершает возвратно-поступательное движения.

Тогда: х = е(1- cos α) + r(1- cos ωt) *

r sin ωt = е sin α => sin α =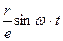

cos α =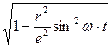

выражение разложим в степенной ряд (ряд Тейлора)

= 1-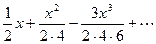

Возьмем два члена ряда и запишем: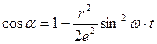

Подставим это в предыдущее выражение * и получим:

Т.к. , то

;

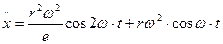
тогда: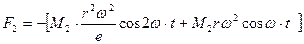

(39)

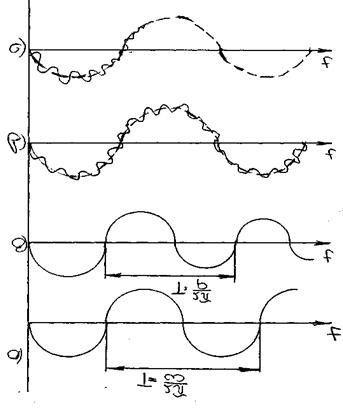
Обобщенная периодическая сила F(t) есть сумма двух слагаемых, первое из которых имеет круговую частоту равную частоте вращения вала двигателя ω, второе слагаемое имеет частоту равную 2 ω.

Таким образом, существует две критических частоты вращения вала двигателя:

Дата добавления: 2015-04-24