Основные цели и задачи динамических расчетов, механических систем с учетом упругости звеньев. 3 страница

ω= р;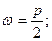

Соответствующим подбором пружины, можно собственную частоту р удалить от указанных критических значений.

Следует помнить, что для F₂ выражение было получено с учетом двух первых членов ряда Тейлора, т.е. более точное выражение для F(t) будет содержать ещё большее число гармоник. Правда, их влияние на поведение системы будет незначительным, и при инженерных расчетах их не учитывают.

Суммарное действие составляющих обобщенной силы в случае исследования линейных систем рассматривают исходя из принципа суперпозиций (принцип наложения) - результирующая движение линейной системы обусловлена одновременным приложением двух или более возмущений, представляет собой линейную сумму движений, как если бы каждое из возмущений действовало бы на систему по отдельности.

Сумма двух гармонических движений одинаковой частоты, но с различными фазовыми углами так же образует гармоническое движение с той же частотой. Сумма же двух гармонических движений различной частоты не является гармоническим движением – это периодическое движение.

В общем случае периодическую возмущающую силу произвольного вида можно представить в виде тригонометрического ряда Фурье.

F(t) = a₀+a₁ · cos ωt+a₂ · cos 2ωt+a₃ · cos 3ωt+ …b₁ · sin ωt+b₂ · sin 2ωt+b₃ · sin 3ωt+… (40)

Тогда уравнение установившихся вынужденных колебаний с демпфированием запишется:

(41)

т.е. в роли возмущающей силы выступает обобщенная периодическая сила произвольного вида. Период этой силы ;коэффициенты а₀, а_i,b_i постоянные, их требуется определять; i- целое число.

Общее решение уравнения (41) из двух частей, первая описывает свободное колебание, вторая – вынужденное. Свободные – затухают, т.к. система демпфирована. Вынужденные будут представлять собой наложенные по принципу суперпозиций установившиеся вынужденные колебания от каждого члена ряда Фурье.

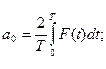
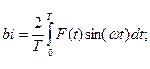(42)

Пример: Возмущающая нагрузка задана периодической функцией. Определить гармонические составляющие этой функции.

Для любого цикла функцию можно выразить:

Графически: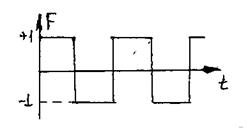

Определить гармонические составляющие этой функции.

1)Определяем значение коэффициентов а₀, а_i, b_i:

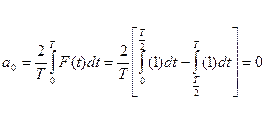
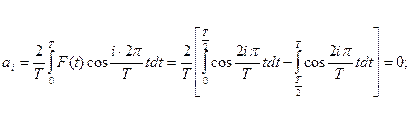
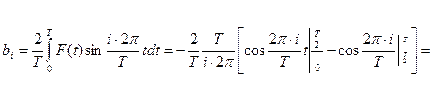
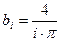, i =1,3,5,7… -нечетные, i= четные.

где i=1,3,5,7…нечетные

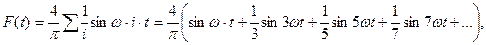
Таким образом, периодическую функцию возмущающей силы раскладывают на простые составляющие, получая гл.формы колебаний. С их помощью сложную результирующую движения удается представить в виде суммы простых гармонических движений, т.е. проводить гармонический анализ какого-то периодического движения. Так, в рассмотренном примере кривая прямоугольного колебательного процесса хорошо приближается тремя первыми гармониками (гармонические составляющие).

21

ВОЗМУЩАЮЩАЯ СИЛА ПРОИЗВОЛЬНОГО ВИДА.

Возмущающие силы, действующие на механические системы, могут меняться и не по периодическому закону, а иметь произвольный вид.

Рассмотрим случай действия такой силы на систему с одной степенью свободы.

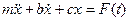делим на т

,

где: q = f(t^/) – возмущающая сила, отнесенная к единице массы

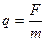
qdt^/ - приращение импульса данной силы, который можно определить в произвольный

момент времени t^/.

Этот импульс сообщает единице массы мгновенное увеличение скорости (приращение скорости)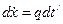

Рассматривая это приращение скорости как начальную скорость в момент t, получим приращение перемещения системы в любой момент времени t, используя выражение (26)

,

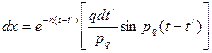т.к. такой же эффект вызывается каждым приращением импульса qdt^/ на интервале t^/=0, t^/=t; то в результате непрерывного действия возмущающей силы q, получим выражение для полного перемещения системы с одной степенью свободы

(43) - интеграл Дюамеля

Это выражение полного перемещения при действии возмущающей силы q – произвольного вида на интервал времени от 0 до t. Оно включает как установившиеся, так и неустановившиеся формы колебаний. Если функцию q = f(t^/) нет возможности выразить аналитически как периодическую, то интеграл всегда можно вычислить приближенно или решить графическим интегрированием.

Если демпфирование в системе не учитывать, т.е. когда п=0, а p_g=p, то интеграл Дюамеля запишется: (44)

Тогда при наличии начального смещения х₀ и начальной скорости , в момент времени t=0 общее решение уравнения сводных колебаний системы без демпфирования запишется:

(45)

рассмотрим пример внезапного приложения сосредоточенной массы постоянной силы F₁. Подобный характер динамического нагружения описывается ступенчатой функцией.

; ;

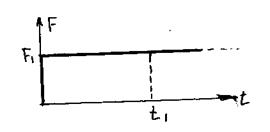
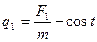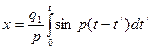При внезапном приложении постоянной по величине силы F₁ возникают колебания с амплитудой , наложенные на статическое смещение той же величины :

(46)

Таким образом, максимальное перемещение, возникающее при внезапном приложении силы в два раза больше перемещения, обусловленного статическим приложением силы.

ПОСТРОЕНИЕ АМПЛИТУДНО-ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ (Аφх)

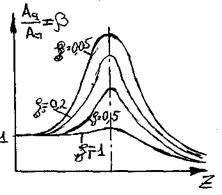
I случай.

Рассмотрим случай, когда ω ≤ р, т.е. частота возмущающей нагрузки, навязанная частота колебаний мала по сравнению с р. β при этом незначительно отличается от 1, т.е. перемещения совпадают с перемещением вектора возмущающей силы.

II случай.

ω ≥ р, значение β близко к 0 и не зависит от степени демпфирования, т.е. высокочастотная возмущающая нагрузка практически не вызывает вынужденных колебаний системы с низким значением собственной частоты. Т.о.для I и II случаев при решении инженерных практических задач допустимо демпфир. системы не учитывать.

А именно при 0,7 ≤ z ≤ 1,3 демпфирование учитывают, т.е. когда система попадает в резонансный коридор.

ПОСТРОЕНИЕ ФАЗОЧАСТОТНОЙ ХАРАКТЕРИСТИКИ (Фφх)

Т.к. возмущающая сила изменяется в соответствии с функцией cos ω t, а вынужденные колебания происходят согласно выражению cos (ω ·t –Θ), то можно сказать, что реакция (поведение) системы отстает от функции возмущающей силы на угол Θ, т.е. когда вектор возмущающей силы направлен вниз, масса, на которую он приложен и на которую он действует, ещё не достигла самого нижнего положения, это будет через время , когда вектор будет отклонен от вертикальной оси на угол Θ.

При отсутствии демпфирования вынужденные колебания в точности совпадают по фазе с колебаниями возмущающей силы при z ≤ 1; при z >1 колебания разделяются на половину цикла, при ω = р ( z = 1) Θ не определяем.

(38)

При демпфировании независимо от величины ξ в случае резонанса имеем ,

т.е. вынужденные колебания отстают от возмущающей силы на четверть цикла.

Для значений z удаленных от резонанса, малый коэффициент демпфирования ξ оказывает незначительное влияние на величину фазового угла Θ, т.е. для значений z значительно меньших 1 Θ практически равен 0, а при z > 1 Θ = π.

Таким образом, за исключением областей, лежащих вблизи резонанса, влияние демпфирования на фазовый угол, так же как и в случае Аφх β( z ) можно не принимать во внимание.

Рассмотрим момент времени t₁, окончание действия силы F₁:

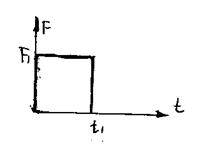
т.е. сила задана в виде прямоугольного импульса.

Рассмотрим два отрезка времени:

в промежуток времени 0≤t≤t₁ 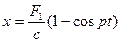- поведение системы описывается таким уравнением.

Когда же t≥ t₁, рассмотрим момент времени t₁

^(*) - начальное смещение (х₀) в момент времени t₁.

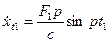^(**) – начальная скорость.

Это начальная скорость, т.е. мы начинаем следить за системой в начальный момент времени t₁, момент окончания действия возмущающей силы F_1.

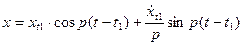(47)

подставим уравнения (*) и (**) в уравнение (47) и получим:

(48)

уравнение движения системы 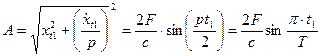(49)

Результирующее движение системы при свободных колебаниях получим в виде выражения (48), амплитуду свободных колебаний, возникших после действия прямоугольного импульса, в виде выражения (49).

Амплитуда свободных колебаний системы, следовательно (уравнение 49) после прекращения действия силы зависит от отношения ,

где t₁ – длительность действия силы,

Т - период свободных колебаний системы.

Рассмотрим действие системы при 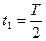, при этом 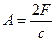, имеет максимальное значение, кроме того действие силы F от 0 до А совпадает с направлением перемещения системы и сила F совершает при этом положительную работу, а т.к. система не демпфирована, то она использует этот запас энергии для совершения свободных колебаний с амплитудой

1)

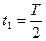
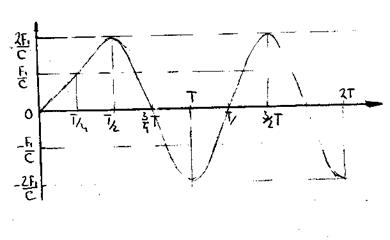
2) t = Т

Рассмотрим второй случай, когда время действия силы t₁=Т. Подставим значение t₁ в (49), тогда А=0, т.е. амплитуда свободных колебаний равна 0 и, действительно, при движении системы от 0 до А сила совершает положительную работу, а при движении системы от А до 0 – отрицательную по знаку работу, т.е. полная совершённая работа равна 0, и система останется в покое после прекращения действия силы.

Рассматриваемый процесс тождественно описывает процессы разгона и торможения механических приводов, когда на систему действуют возмущения в виде ступенчатых функций, крутящеразгоняющий и тормозящий моменты. При рассмотрении этих процессов определяют, что максимальное отклонение от программного движения или наибольшая динамическая ошибка механизма равна т.е. наибольшая ошибка возникает на первой собственной форме колебаний, а затем ошибки резко убывают с ростом собственных форм.

После окончания разгона в системе начнутся свободные колебания, т.к. F=f(t), то ошибка в установившемся режиме будет зависеть от момента окончания разгона, т.е. от длительности действия возмущающей силы, крутящего момента.

график ошибок с учетом трения

27,29

ЧАСТОТНЫЙ АНАЛИЗ МЕХАНИЧЕСКИХ СИСТЕМ
С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ

Рассмотрим частный случай: N=2

Запишем в общем виде дифференциальное уравнение свободных колебаний:

(*)

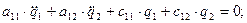
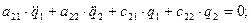
математическая модель в форме уравнений Лагранжа 2-го рода с записью кинетической и потенциальной энергии в квадратичной форме.

Частное решение ищем в виде уравнений, описывающих свободное колебание, т.е.:

(**)

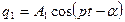
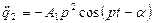
т.е. предполагаем, что обе координаты q₁ и q₂ совершают гармонические колебания с одинаковой частотой р, в фазе или противофазе.

Подставим уравнение (**) в систему уравнений (*), сократим общий множитель и получим уравнение для определения амплитуд:

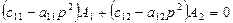
(60)

Уравнение (60) имеет смысл, т.е. не нулевые значения для А₁ и А₂ , если определитель системы равен 0

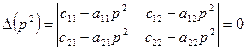(61) -это частотный определитель, который используют для определения собственных частот.

В данном случае после раскрытия определителя получим биквадратное уравнение относительно р ².

Проведя замену р ² = х, получим уравнение, решив его р ₁< р ₂;

р ₁ – основная частота, первая гармоника, основной тон.

Для рассматриваемого случая N=2, каждая из обобщенных координат участвуют в сложном колебательном движении, т.е. движение масс не является простым гармоническим движением, а состоит из двух составляющих с разными частотами р ₁ и р ₂, сложение которых дает периодическое движение, т.е. ; ;

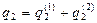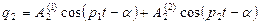(62)

Амплитуды и фазовые углы гармонических составляющих задаются начальными условиями, т.е. амплитуды непосредственно из уравнения (60) определиться не могут, но отношения амплитуд определяются из уравнения (60) и называются коэффициентами формы, независящими от начальных условий (зависят от параметров системы).

Из уравнения (60)

;

;

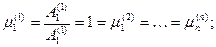
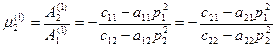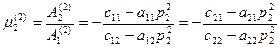т.е.: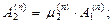

тогда выражение (62) примет вид: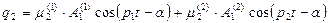

При соответствующем подборе начальных условий возможно колебания всей системы на одной из собственных частот. Эти частные случаи движения называются главными формами колебаний. Колебания на первой частоте называются первой формой колебаний, на второй частоте – второй формой колебаний. Если начальные условия таковы, что

то движения, описываемые первой формой колебаний, имеют вид:

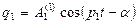
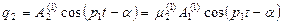(63)

аналогично при

(64)

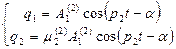
Эпюры, изображающие графически эти системы уравнений (63) и (64) называются графиками собственных форм колебаний:

При построении графиков собственных форм используется принцип суперпозиций, т.е. рассматривается поведение на каждой частоте в отдельности. Из кривых перемещения масс видно, что при первой форме колебаний q₁ и q₂ имеют постоянное отношение амплитуд и совпадают по фазе при положительном μ ₁

При второй форме колебаний перемещения так же всегда постоянны, но совершается в противофазе, разность фаз 180°, отношение амплитуд μ ₂ отрицательно

28,30

1) Составляем выражение для кинетической и потенциальной энергий:

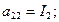
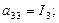
2) Определяем коэффициенты:

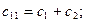
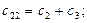
3) Записываем уравнение Лагранжа

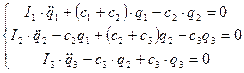(65)

4) Подставим в уравнение Лагранжа выражение для q и (см. систему с N=2).

Сокращаем общий множитель , получаем уравнение относительно р ₁, р ₂, р _3;

Данная система имеет смысл, если её определитель равен 0:

Раскрыв определитель 3-го порядка, решаем бикубическое уравнение относительно р ² и находим р ₁, р ₂, р ₃; р ₁ < р ₂ < р ₃ .

5) Для проверки правильности расчетов при определении р ₁, р ₂, р ₃ строим графики собственных форм колебаний, для чего определим коэффициенты форм µ;

µ ₂ определим из 1-го уравнения:

Сгруппировав множители перед амплитудами, получим определитель:

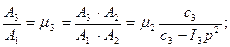
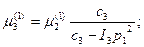
При правильном определении собственных частот р ₁, р ₂, р ₃ на первой форме узлов нет, на второй форме – 2 узла, т.е. число узлов на каждой форме равно номеру частоты – 1.

(На первой частоте – нет узлов, на второй – 1 узел).

ПОЗИЦИОННЫЕ И ЦИКЛИЧЕСКИЕ КООРДИНАТЫ,
ЧИСЛО СОБСТВЕННЫХ ЧАСТОТ ДИНАМИЧЕСКОЙ МОДЕЛИ

Рассмотрим исходную схему ременной передачи:

1) Определим число степеней свободы N=2

2) Найдем выражение для обобщенных координат

φ₁ = q₁; µ₂ = q₁ + q₂; q₂ = φ₂ – φ₁;

3) Определим выражение для собственных частот

Позиционной – называется обобщенная координата, если она не может быть исключена из выражения потенциальной энергии. Остальные обобщенные координаты - циклические.

Запишем выражение для потенциальной и кинетической энергии:

;

;

;

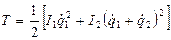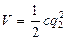4) Определяем коэффициенты

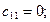
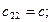
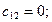
Запишем частотный определитель:

Раскрываем:

После преобразований получим:

;

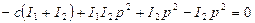
Вывод: Число собственных частот колебаний любой механической системы равно числу позиционных обобщенных координат.

Приближенные методы определения низшей собственной круговой частоты механической системы с n степенями свободы (метод Релея и Донкерлея)

Если консервативная система совершает колебания на одной из своих главных форм то все ее массы движутся с соответствующей основной частотой. Приближенные методы основаны на: 1 принципе суперпозиции.

2 на законе сохранения полной механической энергии консервативной механической системы.

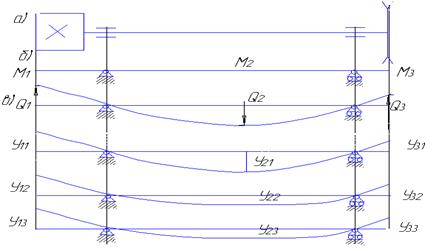
Рассмотрим поперечные изгибные колебания механической системы типа статический определимая балка. Рассмотрим колебания всех масс на первой главной форме колебаний для апраксомации, которой применяют кривую динамического прогиба.

а) – исходная схема

б) – расчетная динамическая модель с сосредоточенными массами

m₁ ­­­­­­– масса консоли вала шпинделя и шкива ременной передачи.

m₂ – сосредоточенная масса участка вала расположенного между опорами

m₃ – масса пилы и консоли

Схема включает массы сосредоточенные на безинерционном блоке

в) – динамическая кривая прогиба балки на первой форме колебаний

где: Q_i – приведенные силы веса участков вала и деталей расположенных на нем

у₁, у₂, у₃ – прогибы в сечениях приложения сил веса.

Прогибы учитываются без учета знака по абсолютной величине.

Дата добавления: 2015-04-24