Аналитический метод

Методы локализации корней

Алгебраические и трансцендентные уравнения

Рассмотрим уравнение f (x) = 0, где функция f (x) определена и непрерывна в не­­­котором конечном или бесконечном интервале a < x < b.

Определение 2.1. Корнем уравнения f (x) = 0 называется значение ξ, обращающее функцию f (x) в нуль, т.е. такое, что f (ξ) = 0.

Определение 2.2. Уравнение f (x) = 0 называется алгебраическим, если функция f (x) является многочленом f (x) = P_n (x) = a_nxⁿ + a_{n – 1} x^{n – 1} + … a ₁ x + a ₀, в противном случае уравнение f (x) = 0 называется трансцендентным.

Встречающиеся на практике уравнения часто не удается решить аналитическими методами. Для решения таких уравнений используются численные методы.

Алгоритм нахождения корня уравнения с по­мощью численного метода состоит из двух этапов:

а) отделение или локализация корня, т.е. установление промежутка
[ a, b ], в котором содер­жит­ся ровно один корень;

б) уточнение значения корня методом последовательных приближений.

Теоретической основой алгоритма отделения корней служит теорема Коши [11] о промежуточных значениях непрерывной функции:

Теорема 2.1. Если функция f (x) непрерывна на отрезке [ a, b ] и f (a) = A, f (b) = B, то для любой точки C, лежащей между A и B на этом отрезке существует точка 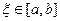, что f (ξ) = C.

Следствие. Если функция f (x) непрерывна на отрезке [ a, b ] и на его концах принимает значения разных знаков, то на этом отрезке существует хотя бы один корень уравнения f (x) = 0.

Пусть область определения и непрерывности функции является конечным отрезком [ a, b ]. Разделим отрезок на n частей:

a_k = a + kh, k = 0, 1, … n, h = (b – a)/ n.

Вычисляя последовательно значения функции в точках a ₀, a ₁, … a_n, находим такие отрезки [ a_k, a_{k +1}], для которых выполняется условие

f (a_k)∙ f (a_{k +1}) < 0, (2.1)

т.е. f (a_k) < 0, f (a_{k +1}) > 0 или f (a_k) > 0, f (a_{k +1}) < 0. Эти отрезки и содержат хотя бы по одному корню.

Пример 2.1. Отделить корни уравнения sin5 x + x ² – 1 = 0.

Решение. Построим таблицу значений функции y = sin5 x + x ² – 1 на отрезке [–4; 4] с шагом изменения аргумента h = 1, пользуясь калькулятором или электронными таблицами (табл. 2.1).

Табл. 2.1

x	–4	–3	–2	–1
y	14,087	7,349	3,544	0,958	–1	–0,958	2,455	8,650	15,912

Табл. 2.1 показывает, что данное уравнение имеет корни в интервалах
(–1; 0) и (1; 2), так как функция меняет знак в этих промежутках. Пока мы не можем утверждать, что в найденных интервалах содержится ровно по одному корню и, что в других интервалах корней нет. Чтобы уточнить информацию о числе корней можно построить таблицу значений функции с меньшим шагом, например h = 0,1.

Теорема 2.2. Если непрерывная функция f (x) монотонна на отрезке
[ a, b ] и на его концах принимает значения разных знаков, то на этом отрезке существует единственный корень уравнения f (x) = 0.

Если функция f (x) дифференцируема и её производная сохраняет знак на отрезке [ a, b ], то f (x) монотонна на этом отрезке.

Если производная 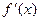легко вычисляется и нетрудно определить её корни, то для отделения корней уравнения f (x) = 0 можно применить следующий алгоритм:

1) Найти критические точки, т.е. точки, в которых производная 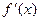равна нулю или не существует, и определить интервалы знакопостоянства производной 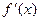(на этих интервалах функция f (x) может иметь только по одному корню);

2) Составить таблицу знаков функции f (x), приравнивая переменную x критическим и граничным значениям, или близким к ним;

3) Определить отрезки, на концах которых функция принимает значения разных знаков.

Пример 2.2. Отделить корни уравнения sin x + x – 1 = 0.

Решение. Найдем производную функции f (x) = sin x + x – 1 и её корни:

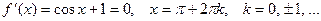
Функция f (x) = sin x + x – 1 монотонна на отрезках [– π + 2π k, π + 2π k ]. Очевидно, что лишь отрезок [– π, π] содержит корень и он единственный.

Дата добавления: 2015-04-25