Метод хорд

Метод хорд [7] заключается в замене кривой y = f (x) отрезком прямой, проходящей через точки (a, f (a)) и (b, f (b)) (см. рис. 2.6). Абсцисса точки пересечения прямой с осью OX принимается за очередное приближение.

Чтобы получить расчетную формулу метода хорд, запишем уравнение прямой, проходящей через точки (a, f (a)) и (b, f (b)) и, приравнивая y нулю, найдем x:

.

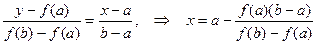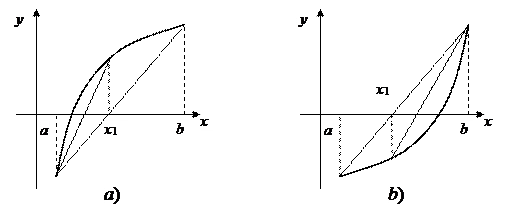
Рис.2.6. Метод хорд

Алгоритм метода хорд:

1) Пусть k = 0;

2) Вычислим следующий номер итерации: k = k + 1; Найдем очередное k -ое приближение по формуле: x_k = a – f (a)(b – a)/(f (b) – f (a)); Вычислим f (x_k).

3) Если f (x_k)= 0 (корень найден), то переходим к 5).

Если f (x_k) f (b) > 0, то b = x_k, иначе a = x_k.

4) Если | x_k – x_{k -1}| > ε, то переходим к шагу 2);

5) Выводим значение корня x_k.

6) Конец.

Замечание. Действия третьего пункта аналогичны действиям метода половинного деления. Однако в методе хорд на каждом шаге может сдвигаться один и тот же конец отрезка (правый или левый), если график функции в окрестности корня выпуклый вверх (рис. 2.6, a)) или вогнутый вниз (рис. 2.6, b)). Поэтому в критерии сходимости используется разность соседних приближений.

Пример 2.6. Применим метод хорд к уравнению sin 5 x + x ² – 1 = 0 и отрезку [0,2; 0,3] для определения корня с точностью до ε = 0,001.

Решение. Проведем расчеты в программе Excel:

1) В ячейки A1:H1 запишем заголовки столбцов как в табл. 2.6;

2) В ячейку B3 запишем формулу =ЕСЛИ(C2*E2<0;B2;D2) и затем ячейку B3 протянем маркером заполнения до ячейки B10;

3) В ячейку C2 запишем формулу =SIN(5*B2)+B2^2-1 и затем ячейку C2 протянем маркером заполнения до ячейки C10;

4) В ячейку D2 запишем формулу =B2-C2*(F2-B2)/(G2-C2) и затем ячейку D2 протянем маркером заполнения до ячейки D10;

5) В ячейку E2 запишем формулу =SIN(5*D2)+D2^2-1 и затем ячейку E2 протянем маркером заполнения до ячейки E10;

6) В ячейку F3 запишем формулу =ЕСЛИ(C2*E2<0;D2;F2) и затем ячейку F3 протянем маркером заполнения до ячейки F10;

7) В ячейку G2 запишем формулу =SIN(5*F2)+F2^2-1 и затем ячейку G2 протянем маркером заполнения до ячейки G10;

8) В ячейку H2 запишем формулу =ABS(F2-B2) и затем ячейку H2 протянем маркером заполнения до ячейки H10;

В таблице 2.8 приведены результаты. Необходимая точность достигается на шаге k = 4.

Таблица 2.8

	A	B	C	D	E	F	G	H
	k	a	f(a)	x	f(x)	b	f(b)	|b-a|
		0,2	-0,11853	0,25753165	0,026506	0,3	0,0874949	0,1
		0,2	-0,11853	0,24701739	0,005194	0,25753165	0,026506	0,01051
		0,2	-0,11853	0,24504339	0,000926	0,24701739	0,0051944	0,00197
		0,2	-0,11853	0,24469436	0,000162	0,2450434	0,0009256	0,00035

Решение в программе Mathcad:

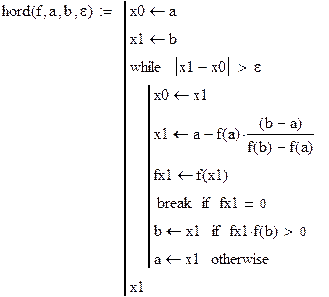
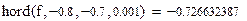
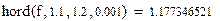
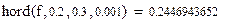
Как видим, результаты расчетов согласуются с предыдущими ответами.

Приведем программу, которая реализует метод хорд на языке C ++:

#include <iostream.h>

#include <math.h>

double f(double x);

typedef double (*PF)(double);

double hord(PF f,double a, double b,double eps, int Kmax);

int main(){

double a, b, x, eps;PF pf; int Kmax;

cout << "\n a = "; cin >> a;

cout << "\n b = "; cin >> b;

cout << "\n eps = "; cin >> eps;

cout << "\n Kmax = "; cin >> Kmax;

pf = f;

x = hord(pf,a,b,eps, Kmax); cout << "\n x = " << x;

cout << "\n Press any key & Enter "; cin >> a;

return 0;

}

double f(double x){

double r;

r = sin(5*x)+x*x-1;

return r;

}

double hord(PF f, double a, double b,double eps,int Kmax){

double xk, xk1, xerr; int k = 0;

xk = a;

do{ k = k + 1; if(k > Kmax)break;

xk1 = a - f(a)*(b - a)/(f(b) - f(a));

if (f(xk1) == 0) break;

xerr = fabs(xk1 - xk); xk = xk1;

if (f(xk1)*f(b) > 0) b = xk1;

else a = xk1;

}while (xerr > eps);

return xk1;

}

Результат расчета для примера 2.6:

a = 0.2

b = 0.3

eps = 0.0001

Kmax = 100

x = 0.244633

Press any key & Enter

Как видим, результат совпадает с предыдущими расчетами.

Дата добавления: 2015-04-25