Метод половинного деления

Методы уточнения корней

После того как найден интервал, содержащий корень, применяют итерационные методы уточнения корня с заданной точностью.

Метод половинного деления (другие названия: метод бисекций, метод дихотомии) для решения уравнения f (x) = 0 заключается в следующем [7, 9]. Пусть известно, что функция непрерывна и принимает на концах отрезка
[ a, b ] значения разных знаков, тогда корень содержится в интервале (a, b). Разделим интервал на две половины и дальше будем рассматривать ту половину, на концах которой функция принимает значения разных знаков. Этот новый отрезок снова делим на две равные части и выбираем из них ту, которая содержит корень. Этот процесс продолжается до тех пор, пока длина очередного отрезка не станет меньше требуемой величины погрешности. Более строгое изложение алгоритма метода половинного деления:

1) Вычислим x = (a + b)/2; вычислим f (x);

2) Если f (x) = 0, то переходим к пункту 5;

3) Если f (x)∙ f (a) < 0, то b = x, иначе a = x;

4) Если | b – a | > ε, переходим к пункту 1;

5) Выводим значение x;

6) Конец.

Пример 2.4. Уточнить методом бисекций с точностью до 0,01 корень уравнения (x – 1)³ = 0, принадлежащий отрезку [0,95; 1,1].

Решение в программе Excel:

1) В ячейках A 1: F 4 введем обозначения, начальные значения и формулы, как показано в таблице 2.3.

2) Каждую формулу скопируем в нижние ячейки маркером заполнения до десятой строки, т.е. B 4 — до B 10, C 4 — до C 10, D 3 — до D 10, E 4 — до E 10, F 3 — до F 10.

Таблица 2.3

	A	B	C	D	E	F
		f(a)=	=(1-B3)^3
	k	a	x	f(x)	b	b-a
		0,95	=(B3+E3)/2	=(1-C3)^3	1,1	=E3-B3
		=ЕСЛИ(D3=0;C3; ЕСЛИ(C$1*D3<0;B3;C3))			=ЕСЛИ(C$1*D3>0; E3;C3)

Результаты расчетов приведены в табл. 2.4. В столбце F проверяем значения длины интервала b – a. Если значение меньше чем 0,01, то в данной строке найдено приближенное значение корня с заданной погрешностью. Потребовалось 5 итераций для достижения требуемой точности. Приближенное значение корня с точностью до 0,01 после округления до трех знаков равно 1,0015625 ≈ 1,00.

Таблица 2.4

	A	B	C	D	E	F
		f(a)=	0,000125
	k	a	x	f(x)	b	b-a
		0,95	1,025	-2E-05	1,1	0,15
		0,95	0,9875	2E-06	1,025	0,075
		0,9875	1,00625	-2E-07	1,025	0,0375
		0,9875	0,996875	3,1E-08	1,00625	0,0187
		0,996875	1,0015625	-4E-09	1,00625	0,0094
		0,996875	0,9992188	4,8E-10	1,0015625	0,0047
		0,99921875	1,0003906	-6E-11	1,0015625	0,0023
		0,99921875	0,9998047	7,5E-12	1,000390625	0,0012

Приведенный алгоритм учитывает возможный случай «попадания в корень», т.е. равенство f (x) нулю на очередном этапе. Если в примере 2.3 взять отрезок [0,9; 1,1], то на первом же шаге попадаем в корень x = 1. Действительно, запишем в ячейке B 3 значение 0,9. Тогда таблица результатов примет вид 2.5 (приведены только 2 итерации).

Таблица 2.5

	A	B	C	D	E	F
		f(a)=	0,001
	k	a	x	f(x)	b	b-a
		0,9			1,1	0,2

Создадим в программе Excel пользовательские функции f(x) и bisect(a, b, eps) для решения уравнения методом половинного деления, пользуясь встроенным языком Visual Basic. Их описания приведены ниже:

Function f(Byval x)

f = (x - 1) ^ 3

End Function

Function bisect(a, b, eps)

1 x = (a + b) / 2

If f(x) = 0 Then GoTo 5

If f(x) * f(a) < 0 Then

b = x

Else

a = x

End If

If Abs(a - b) > eps Then GoTo 1

5 bisect = x

End Function

Функция f(x) определяет левую часть уравнения, а функция
bisect(a, b, eps) вычисляет методом половинного деления корень уравнения f (x) = 0. Обратим внимание на то, что в функции bisect(a, b, eps) используется обращение к функции f(x). Приведем алгоритм создания пользователькой функции:

1) Выполним команду меню «Сервис — Макрос — Редактор Visual Basic». Откроется окно «Microsoft Visual Basic». Если в данном файле программы Excel ещё не были созданы макросы или пользовательские функции или процедуры, это окно будет иметь вид, изображенный на рис.2.4.

Рис. 2.4.

2) Выполним команду меню «Insert — Module» и вводим тексты программ-функции, как показано на рис 2.5.

Рис.2.5.

Теперь в ячейках листа программы Excel можно в формулах использовать созданные функции. Например, введем в ячейку D 18 формулу

=bisect(0,95;1;0,00001),

то получим значение 0,999993896.

Чтобы решить другое уравнение (с другой левой частью) нужно перейти в окно редактора с помощью команды «Сервис — Макрос — Редактор Visual Basic» и просто переписать описание функции f(x). Например, найдем с точностью до 0,001 корень уравнения sin5 x + x ² – 1 = 0, принадлежащий интервалу (0,4; 0,5). Для этого изменим описание функции

Function f(x)

f = (x - 1) ^ 3

End Function

на новое описание

Function f(x)

f = Sin(5 * x) + x ^ 2 - 1

End Function

Тогда в ячейке D 18 получим значение 0,441009521 (сравните этот результат со значением корня из интервала (0,4; 0,5), найденным в примере 2.3!).

Для решения уравнения методом половинного деления в программе Mathcad создадим подпрограмму-функцию bisec (f, a, b, ε), где:

f — имя функции, соответствующее левой части уравнения f (x) = 0;

a, b — левый и правый концы отрезка [ a, b ];

ε — точность приближенного значения корня.

Решение примера в программе Mathcad:

1) Запускаем программу Mathcad. Введем определение функции bisec (f, a, b, ε). Для этого с помощью клавиатуры и панели инструментов «Греческие символы» набираем bisec (f, a, b, ε):=. После знака присваивания «:=» на панели инструментов «Программирование» указателем мыши щелкаем левой кнопкой «Add line». После знака присваивания появится вертикальная линия. Далее вводим текст программы, который приведен ниже, используя панель инструментов «Программирование» для ввода знака «←», оператора цикла while, оператора break и условного оператора if otherwise.

2) Введем определение функции f (x):=sin(5*x)+x^2–1, а затем вычислим значение корня с помощью функции bisec при заданных значениях:
bisec (f, –0.8,–0.7,0.0001)=. После знака «=» автоматически появится вычисленное программой значение корня –0,7266601563. Аналогично вычислим остальные корни.

Ниже приведен лист Mathcad с определением функции bisec (f, a, b, ε) и расчетами:

Определим программу-фунцию метода половинного деления:

Зададим функцию f(x)=sin5x+x2-1 и найдем её корни в указанных интервалах с точностью 0,0001:

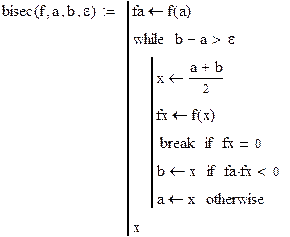
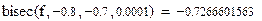
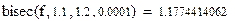
Найденные значения корней согласуются с предыдущими результатами. Если мы определим функцию y (x) = (x – 1)³ и найдем корень в интервале (0,9; 1,1), то получим значение x = 1, так как в этом случае на первом шаге деления получается точное значение корня:

Приведем программу на языке C ++ для решения уравнения f (x) = 0 методом половинного деления:

#include <iostream.h>

#include <math.h>

double f(double x);

typedef double (*PF)(double);

double bisec(PF f,double a, double b,double eps);

int main(){

double a, b, x, eps;PF pf;

cout << "\n a = "; cin >> a;

cout << "\n b = "; cin >> b;

cout << "\n eps = "; cin >> eps;

pf = f;

x = bisec(pf,a,b,eps); cout << "\n x = " << x;

cout << "\n Press any key & Enter "; cin >> a;

return 0;

}

double f(double x){

double r;

r = sin(5*x)+x*x-1;

return r;

}

double bisec(PF f, double a, double b,double eps){

double x;

do{ x = (a + b)/2;

if (f(x) == 0) break;

if (f(x)*f(a)<0) b = x;

else a = x;

}while (fabs(b-a) > eps);

return x;

}

В программе функция f (x) определена для решения уравнения

sin5 x + x ² – 1 = 0

из примера 2.3. Результат работы программы для определения корня из интервала (0,4; 0,5) с точностью 0,00001 представлен ниже (экран компьютера):

a = 0.4

b = 0.5

eps = 0.0001

x = 0.44101

Press any key & Enter

Последняя строка нужна для организации паузы для просмотра результата.

Дата добавления: 2015-04-25