Прямая на плоскости

ТЕМА 2. АЛГЕБРАИЧЕСКИЕ ЛИНИИ ПЕРВОГО И ВТОРОГО ПОРЯДКА.

Алгебраической линией (кривой) п -го порядка называется линия, определяемая алгебраическим уравнением п-й степени относительно декартовых координат.

Линиями первого порядка являются прямые, а к важнейшим линиям второго порядка относятся окружность, эллипс, гипербола, парабола.

Прямую линию на плоскости от­носительно системы декартовых прямо­угольных координат можно задать раз­личными способами. Прямая однозначно определяется углом, образуемым ею с осью Ох, и величиной направленного отрезка, отсекаемого на оси Оу, коорди­натами двух точек и т.п. В зависимости от способа задания прямой рассматри­вают различные виды ее уравнения.

Различные виды уравнения прямой на плоскости.

Из курса математики средней школы известно уравнение пря­мой, пересекающей ось Оу:

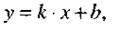(1)

в котором k- угловой коэффициент, определяемый формулой

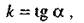
где 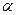- угол между прямой и осью Ох; b = - величина направлен­ного отрезка, отсекаемого прямой на оси Оу. Уравнение (1) называется уравнением прямой с угловым коэффициентом.

Если прямая параллельна оси Ох, т.е. 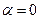, k =0 то уравнение (1) прини­мает вид

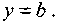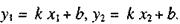Выразим угловой коэффициент прямой (1) через координаты ее двух различных точек 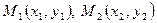. Так как эти точки ле­жат на прямой (1), то их координаты удовлетворяют данному уравнению, т.е.

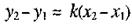Вычитая первое равенство из второго, получаем

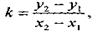Откуда (2)

Пусть заданы угловой коэффициент k прямой и ее точка 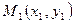. Составим уравнение этой прямой. Зафиксируем произволь­ную точку М(х, у) данной прямой и найдем выражение для ее углового коэффициента по формуле (2), положив в ней у₂= у,

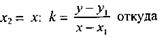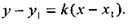(3)

Уравнение (3) называется уравнением прямой, проходящей через данную точку в данном направлении.

Пучком прямых на плоскости называется множество всех пря­мых этой плоскости, проходящих через данную точку (центр пучка).

Составим уравнение прямой, проходящей через две данные раз­личные точки 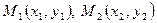где 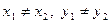. Поскольку эта прямая проходит через точку 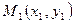, уравнение (3) с учетом фор­мулы (2)

запишется так:

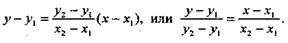(4)

Уравнение (4) называется уравнением прямой, проходящей через две данные точки.

Обозначив равные отношения буквой t, получим

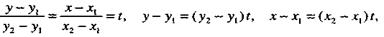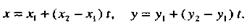(5)

Отметим, что при t= 0 из уравнений (5) получаем координаты точки 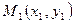, при t= 1 - координаты точки М₂(х₂, у₂), при 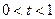- коор­динаты любой внутренней точки отрезка [М₁М₂]; когда t меняется в бесконечном промежутке 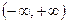, точка М(х, у) описывает рассмат­риваемую прямую. Уравнения (5) называются параметрическими уравнениями прямой..

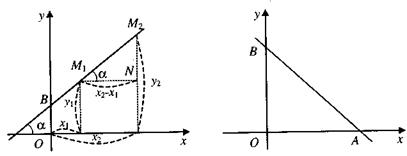
Пусть прямая (АВ) (рис.) отсекает на координатных осях от­резки, величины которых соответственно равны а и b, т.е. О А = а, ОB = b, А(а, 0), B (0, b). Применяя уравнение (4) для этого случая, т.е., полагая х₁= а, у₁= 0, х₂= 0, у₂= b, получаем уравнение в отрезках на осях координат:

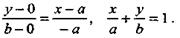(6)

2. Угол между двумяпрямыми. Условия параллельности и перпендикулярности двух прямых.

Рассмотрим две прямые; предположим, что ни одна из них не параллельна оси Оу (рис.). В этом случае прямые можно задать их уравнениями с угловыми коэффициентами

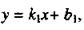(7)

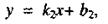(8)

где

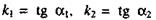(9)

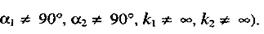(в силу предположения

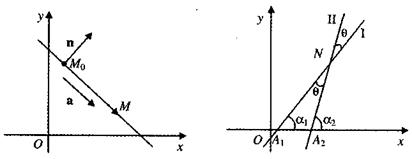
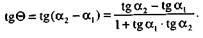Обозначим через 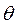угол наклона второй прямой к первой, т.е. угол, на который нужно повернуть вокруг точки пересечения первую из них, чтобы она совпала со второй. Из треугольника A₁A₂N (рис.) следует, что 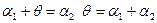поэтому

Подставив выражения (9) в последнее равенство, получим искомую формулу

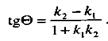
(10)

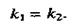Необходимое и достаточное условие параллельности прямых (7) и (8) выражается равенством

(11)

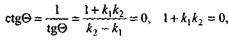Пусть прямые, заданные уравнениями (7) и (8), перпенди­кулярны, т.е. 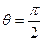, в этом случае 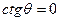, следовательно,

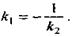откуда

(12)

Если прямые заданы общими уравнениями

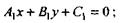(13)

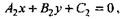(14)

то тангенс угла между ними определяется формулой

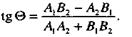(15)

В самом деле, разрешив уравнения (13), (14) относительно у и сравнив их соответственно с уравнениями (7), (8), получим вы­ражения для угловых коэффициентов

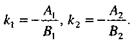(16)

Формула (15) следует из формулы (10) и равенств (16).

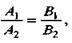Необходимое и достаточное условие параллельности прямых (13) и (14) выражается равенством

(17)

а условие их перпендикулярности – равенством

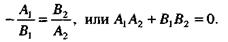(18)

Дата добавления: 2015-04-25