Гипербола и парабола

Определение гиперболы и вывод ее канонического уравнения.

Гиперболой называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек (фокусов) той же плоскости есть величина постоянная.

Обозначим эту постоянную через 2а, расстояние между фокуса­ми F ₁и F ₂ - через 2с (фокусное расстояние). Пусть М - произвольная точка гиперболы, тогда

(34)

Выберем декартову прямо­угольную систему координат так, что­бы ось Ох проходила

через фокусы, а ее положительное направление совпа­дало с направлением отрезка ,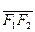

начало поместим в середине этого отрезка. При таком выборе системы координат фокусы будут иметь коор­динаты: 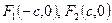. Обозначив текущие координаты точки М через х и у, получим

Уравнение (34) принимает вид

(35)

Уравнение (35) является уравнением гиперболы, так как ему удовлетворяют координаты любой точки гиперболы и только они. Уп­ростим его (тем же способом, что и уравнение (28)), получим

(36)

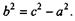где (37)

Уравнение (36) называется каноническим уравнением гиперболы. Гипербола (36) имеет две асимпто­ты:

(38)

Центр симметрии гиперболы называется ее центром. Оси симметрии гиперболы называются просто ее осями, одна ось пере­секает гиперболу в двух точках, называемых вершинами эта ось называется действительной осью гиперболы, другая ось - мнимой осью, она не имеет общих точек с гиперболой. Длины отрезков 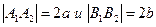также называются осями.

Величины а и b называются полуосями гиперболы. Если а = b, гипер­бола называется равносторонней, ее уравнение

(39)

Уравнение

(40)

определяет гиперболу с действительной осью Оу.

Эксцентриситет гиперболы, фокальные радиусы, директрисы гиперболы.

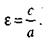Эксцентриситетом гиперболы называется отношение ее фо­кусного расстояния к расстоянию между ее вершинами. Если действи­тельной осью является ось Ох, то по определению

(41)

Так как для гиперболы с > а, то е >1.

Фокальными радиусами точки М гиперболы называются отрез­ки, соединяющие эту точку с фокусами данной гиперболы. Их длины 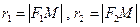выражаются формулами:

для правой ветви (42)

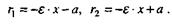для левой ветви (43)

Директрисами гиперболы называются прямые, перпен­дикулярные действительной оси гиперболы и расположенные симмет­рично относительно центра на расстоянии 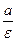от него (а - действи­тельная полуось, 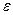- эксцентриситет гиперболы). Если гипербола зада­на каноническим уравнением (36), то в данной системе координат ее директрисы определяются 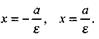уравнениями

Парабола.

Параболой называется множество всех точек плоскости, равно­удаленных от данной точки (фокуса) и данной прямой (директрисы).

Пусть р - расстояние от фокуса F до директрисы 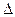. Ось Ох де­картовой прямоугольной системы координат выберем так, чтобы она проходила через F перпендикулярно 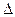, ее положительное направление - от 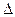к F (рис.), начало координат поместим в середине отрезка ВF, где В - точка пересечения Ох и 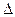. В этой системе координат точки F и В имеют следующие координаты: F (р/2; 0), В(-р/2; 0)

Возьмем произвольную точку М(х, у) параболы, обозначим че­рез r расстояние до фокуса, через d. - расстояние до директрисы (), по определению параболы r=d. Поскольку

то

(44)

Уравнение (44) является уравнением параболы. Возведя по­членно в квадрат это уравнение и приводя подобные члены, получаем

(45)

Уравнение (45) называется каноническим уравнением парабо­лы.

Уравнение директрисы (как прямой, параллельной оси Оу и проходящей через точку 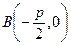) имеет вид .

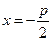Дата добавления: 2015-04-25