В компьютерных технологиях

Работа с числами в других системах счисления, используемых

Пример 15.

Перевести 0.65₁₀ в 2-ю систему счисления с точностью 6 знаков.

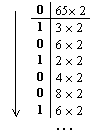Результат: 0.65₁₀ 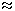0.10(1001)₂

Перевод неправильной десятичной дроби в систему счисления с недесятичным основанием. Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и дробная части исходного числа переводятся отдельно по соответствующим алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой (точкой).

Пример 16.

Перевести 23.125₁₀ в 2-ю систему счисления

1) Переведем целую часть:	2) Переведем дробную часть:

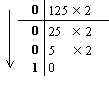
Таким образом: 23₁₀ = 10111₂; 0.125₁₀ = 0.001₂.

Результат: 23.125₁₀ = 10111.001₂.

Необходимо отметить, что целые числа остаются целыми, а правильные дроби – дробями в любой системе счисления.

Восьмеричная ишестнадцатеричная системы счисления являются вспомогательными системами при подготовке задачи к решению.Удобство ее использования состоит в том,что числа соответственно в 3 и 4 раза короче двоичной системы, а перевод в двоичную систему и обратно несложен и выполняетсяпростым механическим способом.

Для того чтобы произвольное двоичное число записать в системе счисления с основанием q =2ⁿ, нужно:

­ данное двоичное число разбить слева и справа (целую и дробную части) на группы по n цифр в каждой;

­ если в последних правой и левой группах окажется меньше n разрядов, то их надо дополнить справа и слева нулями до нужного числа разрядов;

­ рассмотреть каждую группу как n – разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q = 2ⁿ.

Значит для того чтобы произвольное число записать в системе счисления с основанием q = 2ⁿ, т. е. перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n-разрядным эквивалентом в двоичной системе счисления. Применительно к компьютерной информации часто используются системы счисления с основанием 8 (восьмеричная) и 16 (шестнадцатеричная).

Перевод из двоичной в восьмеричную и шестнадцатеричную систему счисления и обратно. Для того чтобы двоичное число записать в восьмеричной системе счисления, необходимо разбить его на триады (т.е. группы по 3 цифры, так как 8 = 2³), начиная от запятой, отделяющей целую часть от дробной части. После этого каждая триада заменяется одной соответствующей ей восьмеричной цифрой. Недостающие справа и слева цифры восполняются нулями. Связь между двоичной и восьмеричной системами счисления приведена в таблице 2.2. Каждой восьмеричной цифре соответствует тройка – тетрада двоичных чисел.

Таблица 2.2 – Двоично-восьмеричная таблица

8-я система счисления	2-я система счисления

Пример 17. Перевести число 1011101,10111₂ в восьмеричную систему счисления.

1011101,10111₂ = ê 001 ê 011 ê 101 ê, ê 101 ê 110 ê = 135,56₈

Перевод двоичных чисел в шестнадцатеричную систему счисления. Для того чтобы двоичное число записать в 16-ричной системе счисления, необходимо разбить его на тетрады (группы из 4 цифр, т.к. 16 = 2⁴), начиная от запятой, в обе стороны. После этого каждая тетрада заменяется соответствующей ей 16-ричной цифрой. В этом случае используется двоично-шестнадцатеричная таблица. Связь между двоичной и шестнадцатеричной системами счисления приведена в таблице 2.3.

Таблица 2.3 – Двоично-шестнадцатеричная таблица.

16-я система счисления	2-я система счисления		16-я система счисления	2-я система счисления
		A
		B
		C
		D
		E
		F

Пример 18. Перевести число 1011101,10111₂ в шестнадцатеричную систему счисления.

1011101,10111₂ = ê0101 ê 1101 ê, ê 1011 ê 1000 ê = 5D,B8₁₆

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления. Для перевода 8-ричного числа в двоичную систему счисления достаточно каждую восьмеричную цифру нужно заменить соответствующей ей двоичной триадой. Для перевода 16-го числа в двоичную систему счисления достаточно каждую шестнадцатеричную цифру заменить соответствующей ей двоичной тетрадой.

Пример 19. Перевести числа в двоичную систему.

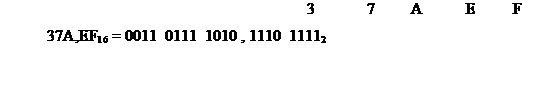
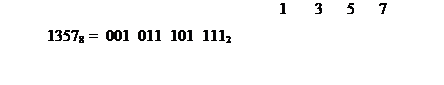
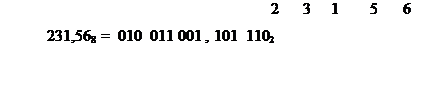
При переходе из 8-ричного счисления в 16-ричное счисление и обратно используется вспомогательный, двоичный код числа.

Пример 20. Перевести восьмеричные числа в шестнадцатеричные и наоборот шестнадцатеричные числа в восьмеричные.

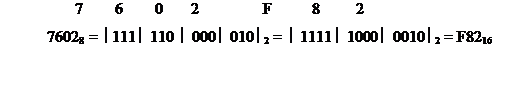
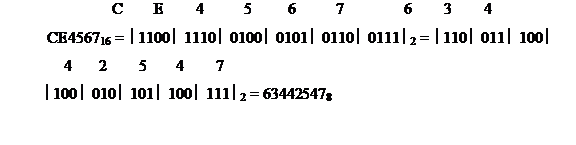
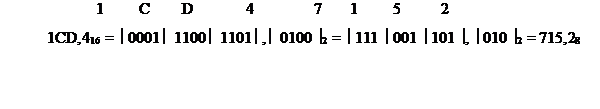
Дата добавления: 2015-04-25