Кодирование и форматы представления числовых данных

Формы представления и преобразования информации

В компьютере используются следующие формы представления числовых данных:

· числа с фиксированной запятой (точкой);

· числа с плавающей запятой (точкой);

Представление чисел в форме с фиксированной запятой (точкой) получило название естественной формы числа, представление с плавающей точкой – нормальной формы числа. Под те или иные форматы всегда отводится заранее известное количество разрядов (бит) - 16, 32, и т.д.

2.3.1.1. Представление чисел в формате с фиксированной точкой. При представлении числа Х в форме с фиксированной точкой указывается знак числа (sign X) и модуль числа (mod X) в q – ичном коде. Место точки (запятой) постоянно для всех чисел и в процессе решения задач не меняется. Знак положительного числа кодируется цифрой 0, знак отрицательного числа – цифрой 1.

Код числа в форме с фиксированной точкой, состоящий из кода знака и q– ичного кода его модуля, называется прямым кодом q – ичного числа. Разряд прямого кода числа, в котором располагается q – ичный код модуля числа, называется знаковым разрядом кода. Разряды прямого кода числа, в которых располагаются q – ичный код модуля числа, называются цифровыми разрядами кода. При записи прямого кода знаковый разряд располагается левее старшего цифрового разряда и обычно отделяется от цифровых разрядов точкой. В общем случае разрядная сетка для размещения чисел в форме с фиксированной точкой выглядит так:

Знак числа

q ^n^-1

q ^1

q ^0,

q ^-1

q^-2

q ^-m

В формате с фиксированной точкой представляются целые числа, в формате с плавающей точкой - вещественные (целые и дробные). Пусть для целых чисел в памяти ЭВМ отводится 2 байта. Формат представления целых чисел выглядит следующим образом:

Номера разрядов

Второй байт

Первый байт

15 Знак числа

Пример 21. Разместитьцелое число Z1 = 283₁₀ .в байтах памяти. Это число положительное, поэтому его знак кодируется как (0). Двоичный код этого числа Z1 = 100011011₂ . Тогда это число в памяти ЭВМ будет расположено так:

Номера разрядов

Второй байт

Первый байт

Пример 22. Разместитьцелое число Z2 = – 21₁₀ . Знак этого числа кодируется как (1), поскольку число отрицательное. Двоичный код этого числа Z2 = 10101₂ . Тогда это число в памяти ЭВМ будет расположено так:

Номера разрядов

Второй байт

Первый байт

2.3.1.2. Представление чисел в формате с плавающей точкой. В формате с плавающей точкой числа представляются в виде мантиссы и основания системы в соответствующей степени. Любое число в этом формате можно представить в виде:

,

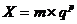(2.10)

где m – мантисса числа; q – основание системы счисления; p – порядок.

Все эти величины – двоичные числа без знака. Для представления чисел в формате с плавающей точкой используются фиксированные форматы разной длины. В разрядной сетке форматов отводятся места для знака мантисс (нулевой разряд). Знака порядка (первый разряд), значение порядка (6 разрядов, со 2-го по 7-й), в остальные записывается мантисса числа. Далее представлена разрядная сетка в формате 4 байта.

Разряды (всего 32 разряда: с 0 – го по 31 – й)

Любое число в формате с плавающей точкой можно представить в различной форме записи.

Пример 23. Представить десятичное число 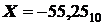в формате с плавающей запятой и разместить в байтах памяти

Х = –55,25 = –5525*10 ^-2 = –0,5525*10 ², здесь мантисса m = –0,5525, а порядок p = 2.

Обычно числа с плавающей точкой записываются в нормализованном виде т. е. в виде: Х = – 0,5525*10 ² . Тогда для числа Х:

· знак мантиссы – отрицательный (–) – кодируется как (1);

· знак порядка – положительный (+) – кодируется как (0);

· мантисса m = 0,5525₁₀ = 0,100011₂ ;

· порядок p = 2₁₀ =10₂ ;

Номера разрядов

Зн m

Зн p

Порядок p

Мантисса m

.

.

.

2.3.1.3. Выполнение арифметических операций с целыми числами, представленными машинными кодами. Для хранения чисел и выполнения различных операций над ними их представляют различными кодами: прямым, обратным и дополнительным. Основные отличия кодов чисел от самих чисел заключаются в следующем:

· разряды числа в коде жестко связаны с определенной разрядной сеткой;

· для записи кода знака в разрядной сетке отводится постоянно строго определенный разряд.

Код числа в форме с фиксированной точкой, состоящий из кода знака и двоичного кода его модуля, называется прямым кодом двоичного числа. Для его записи в разрядную сетку необходимо выполнить следующие операции:

· записать двоичный код целого числа;

· недостающие цифры старших разрядов двоичного кода заменить нулями с тем, чтобы все разряды разрядной сетки были заполнены;

· в старший разряд (8 – й или 16 – й) записать код знака: 0 – для положительного числа и 1 – для отрицательного числа.

Замечание: Обратный и дополнительный коды как правило применяются для кодирования отрицательных чисел.

2.3.1.3.1.Правила образования обратного и дополнительного двоичных машинных кодов. Рассмотрим правила образования двоичных машинных кодов:

1. Положительное число в прямом, обратном и дополнительном кодах выглядят одинаково.

2. Прямой код отрицательных и положительных чисел имеет различное значение только в знаковом разряде, модуль числа не изменяется.

3. Обратный код двоичного отрицательного числа получается из прямого кода путем замены единиц на нули и нулей на единицы, только код знака оставить без изменения.

4.

Пример 24. Представить двоичное число в обратных кодах.

Х2 = +1101101	[Х2]пр = 0.1101101	[Х2]обр = 0.0010010
Х2 = – 0101101	[Х2]пр = 1.0101101	[Х2]обр = 1.1010010

Здесь точкой отделяется знак числа (его код) от двоичного кода самого числа. Для простоты изложения рассматривается восьмиразрядная сетка.

4. Дополнительный код отрицательного числа получается формированием обратного кода отрицательного числа и прибавлением единицы к младшему разряду этого кода (перенос в знаковый разряд при этом теряется).

Пример 25. Представить двоичное число в дополнительных кодах.

Х2 = +1101101	[Х2]пр = 0.1101101	[Х2]доп = 0.1101101
Х2 = -1011001	[Х2]пр = 1.1011001	[Х2]доп = 1.0100110

2.3.1.3.2. Арифметические действия над целыми числами, представленными в обратном или дополнительном машинном коде. При сложении чисел, представленных в естественной форме, необходимо учитывать следующие положения:

· числа хранятся в памяти компьютера в дополнительном коде;

· числа складываются вместе со знаками, при этом формируется знак результата;

· при сложении чисел с разными знаками единица переноса из знакового разряда отбрасывается.

Сложение чисел. При сложении чисел нужно использовать вышеприведённые правила сложения двоичных разрядов (2.9)

Пример 26. Сложить два числа 126₁₀ и 267₁₀. Проверить результат сложения, сделав обратное преобразование.

Проверка.

А=0.000000110001001₂=1*2⁰+0*2¹+0*2²+1*2³+0*2⁴+0*2⁵+0*2⁶+1*

2⁷+1*2⁸+....=393₁₀

Вычитание чисел. Рассмотрим операцию вычитания, которая выполняется следующим образом: определяется дополнительный или обратный код вычитаемого числа и производится сложение этого кода с уменьшаемым числом.

А – В = А + [– В]_{обр-доп}

Вычитание чисел, представленных в обратном коде. Если при выполнении операции сложения чисел формируется перенос из знакового разряда, при использовании обратного кода, он должен быть добавлен в младший разряд результата.

Пример 27. Даны два числа А = 126₁₀ и В = 267₁₀. Найти сумму этих чисел при разных знаках. Результат проверить.

В данном примере при сложении обратных кодов чисел возникает единица переполнения в старшем знаковом разряде, которую необходимо перенести и добавить к младшему разряду полученного результата сложения. В итоге получается двоичный код результата сложения в обратном коде, поскольку в знаковом разряде присутствует 1. Для получения окончательного результата в прямом коде необходимо инвертировать разряды предыдущего результата кроме знакового разряда. Инверсия означает обратное преобразование, т. е. 0 заменяется на 1, а 1 заменяется на 0.

Если в знаковом разряде полученного результата стоит 0, то это означает, что получен прямой код результата, и его не нужно дополнительно инвертировать, как в предыдущем случае.

Проверка.

Вычитание чисел, представленных в дополнительном коде. Рассмотрим правила проведения сложения и вычитания чисел, представленных в дополнительных кодах на конкретном примере.

Пример 28. Даны два десятичных числа А = 26₁₀ и В = 34₁₀. Найти сумму этих чисел при разных знаках. Результат проверить.

Вначале представим числа в двоичном коде:

А = 26 10 = 11010 2

В = 34 10 = 100010 2

В естественной форме в прямом и дополнительном кодах эти числа имеют следующий вид:

При использовании дополнительного кода единица переноса (переполнения) из знакового разряда не принимается во внимание, т.е. отбрасывается.

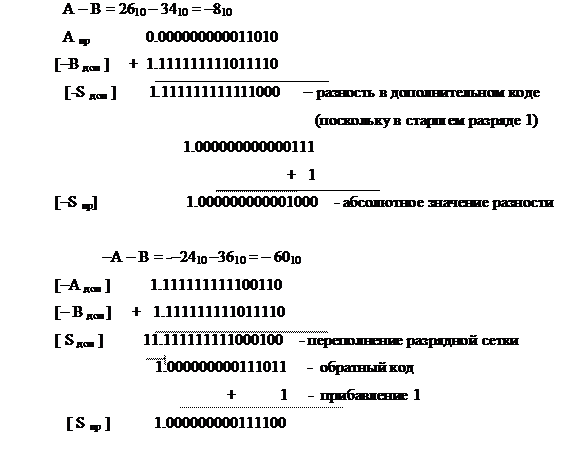
Проверка.

Проверим правильность полученных результатов. Для этого переведем их в десятичную систему счисления.

А + В = 0.000000000111100₂ =

= 0*2⁰+0*2¹+1*2²+1*2³+1*2⁴+1*2⁵+0*2⁶+...= 60₁₀

–А – В = 1.000000000111100₂ =

= – (0*2⁰+0*2¹+1*2²+1*2³+1*2⁴+1*2⁵+0*2⁶+...)= – 60₁₀

А – В = 1.000000000010000₂ = – (0*2⁰+0*2¹+0*2²+0*2³+1*2⁴+.....) = – 8₁₀

– А + В = 0.000000000010000₂ = 0*2⁰+0*2¹+0*2²+0*2³+1*2⁴+..... = 8₁₀

Проверка показывает правильность вычисленных сумм.

Дата добавления: 2015-04-25