Примеры решения задач 3 страница. а для конечного состояния –

p ₁ V =(m ₁/ M) RT ₁, (1)

а для конечного состояния –

p ₂ V =(m ₂/ M) RT ₂, (2)

где m ₁ и m ₂ — массы гелия в начальном и конечном состояниях.

Выразим массы m ₁ и m ₂ гелия из уравнений (1) и (2):

m ₁= Mp₁V /(RT ₁); (3)

m₂=Mp₂V/(RT₂); (4)

Вычитая из (3) равенство (4), получим

.

Отсюда найдем искомое давление:

. (5)

Проверим, дает ли правая часть формулы (5) единицу давления. Для этого выразим все величины, входящие в нее, в соответствующих единицах. Единица, в которой выражается первое слагаемое, не вызывает сомнений, так как отношение T ₂/ T ₁ — величина безразмерная. Проверим, в каких единицах выражается второе слагаемое:

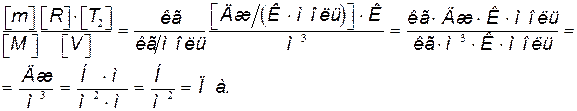
Убедившись в том, что правая часть полученной расчетной формулы дает единицу искомой величины – давления, можем подставить в (5) значения всех величин и произвести вычисления.

В формуле (5) все величины, кроме молярной массы М гелия, известны. Для гелия как одноатомного газа относительная молекулярная масса равна его относительной атомной массе А _r.

Из таблицы Д. И. Менделеева найдем А _r=4. Следовательно, молярная масса гелия М= А _r×10^-3 кг/моль =4×10^-3 кг/моль. Подставив значения величин в (5), получим

.

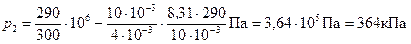Пример 7. Определить количество теплоты, поглощаемой водородом массой m =0,2 кг при нагревании его от температуры t ₁=0°С до температуры t ₂=100 °С при постоянном давлении. Найти также изменение внутренней энергии газа и совершаемую им работу.

Решение. Количество теплоты Q, поглощаемое газом при изобарном нагревании, определяется по формуле

Q=mc_pDT, (1)

где m — масса нагреваемого газа; c_p — его удельная теплоемкость при постоянном давлении; D T — изменение температуры газа.

Как известно, . Подставив это выражение c _p в формулу (1), получим

,

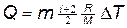где (молекула водорода двухатомная); 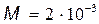кг/моль – молярная масса водорода.

Произведя вычисления по этой формуле, найдем

Q =291 кДж.

Внутренняя энергия выражается формулой 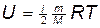, следовательно, изменение внутренней энергии

.

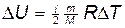После подстановки в эту формулу числовых значений величин и вычислений получим DU =208 кДж.

Работу расширения газа определим по формуле, выражающей первое начало термодинамики: Q=DU+A, откуда

A=Q – DU.

Подставив значения Q и DU, найдем

А =83 кДж.

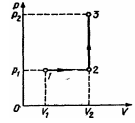
Пример 8. Кислород занимает объем V ₁=1 м³ и находится под давлением р ₁=200 кПа. Газ нагрели сначала при постоянном давлении до объема V ₂=3 м³, a затем при постоянном объеме до давления (рис 20) р ₂=500 кПа. Построить график процесса и найти: 1) изменение DU внутренней энергии газа; 2) совершенную им работу A; 3) количество теплоты Q,переданное газу.

Решение. Построим график процесса (рис. 20). На графике точками 1, 2, 3 обозначены состояния газа, характеризуемые параметрами (р ₁, V ₁, T ₁), (р ₁, V ₂, T ₂),(р ₂, V ₂, T ₃).

1. Изменение внутренней энергии газа при переходе его из состояния 1 в состояние 3 выражается формулой

DU=c_vmDT,

где c _v — удельная теплоемкость газа при постоянном объеме; m — масса газа; D T — разность температур, соответствующих конечному 3и начальному 1 состояниям, т. е. D T = T ₃ – T ₁. Так как ;

где М — молярная масса газа, то

. (1)

Температуры T ₁ и T ₃ выразим из уравнения Менделеева — Клапейрона ():

С учетом этого равенство (1) перепишем в виде

DU=(i/2)(p₂V₂ – p₁V₁).

Подставим сюда значения величин (учтем, что для кислорода, как двухатомного газа, i =5) и произведем вычисления:

DU=3,25 МДж.

2. Полная работа, совершаемая газом, равна A = A ₁+ A ₂, где A ₁ — работа на участке 1—2; A ₂ — работа на участке 2—3,

На участке 1—2 давление постоянно (p =const). Работа в этом случае выражается формулой A ₁= p ₁D V = p ₁(V ₂ – V ₁). На участке 2—3 объем газа не изменяется и, следовательно, работа газа на этом участке равна нулю (A ₂=0). Таким образом,

A=A₁=p₁(V₂—V₁).

Подставив в эту формулу значения физических величин, произведем вычисления:

A=0,4 МДж

3. Согласно первому началу термодинамики, количество теплоты Q, переданное газу, равно сумме работы A, совершенной газом, и изменению D U внутренней энергии:

Q=A+DU, или Q =3,65 МДж.

Пример 9. Идеальный двухатомный газ, содержащий количество вещества 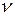=l моль, находится под давлением p ₁=250кПа и занимает объем V ₁==10 л. Сначала газ изохорно нагревают до температуры T ₂=400 К. Далее, изотермически расширяя, доводят его до первоначального давления. После этого путем изобарного сжатия возвращают газ в начальное состояние. Определить термический КПД h цикла.

Решение. Для наглядности построим сначала график цикла, который состоит из изохоры, изотермы и изобары. В координатах р, V этот цикл имеет вид. представленный на рис. 21. Характерные точки цикла обозначим 1, 2, 3.

Термический КПД любого цикла определяется выражением

h=(Q₁ – Q₂)/Q₁, или h =1 – Q₂/Q₁, (1)

где Q ₁ — количество теплоты, полученное газом за цикл от нагревателя; Q ₂ — количество теплоты, отданное газом за цикл охладителю.

Заметим, что разность количеств теплоты Q ₁ – Q ₂ равна работе A, совершаемой газом за цикл. Эта работа на графике в координатах р, V (рис. 21) изображается площадью цикла (площадь цикла заштрихована).

Рабочее вещество (газ) получает количество теплоты Q ₁ на двух участках: Q _1-2 на участке 1—2 (изохорный процесс) и Q _2-3 на участке 2—3 (изотермический процесс). Таким образом,

Q₁=Q_1-2+Q_2-3.

Количество теплоты, полученное газом при изохорном процессе, равно

Q_1-2= C _v 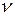(T ₂ – T ₁),

где C _v — молярная теплоемкость газа при постоянном объеме; 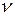— количество вещества. Температуру T ₁ начального состояния газа найдем, воспользовавшись уравнением Клапейрона — Менделеева:

T₁=p₁V₁/(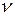 R).

Подставив числовые значения и произведя вычисления, получим

.

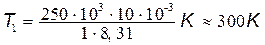Количество теплоты, полученное газом при изотермическом процессе, равно

Q _2-3= 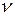RT ₂ln(V ₂/ V ₁),

где V ₂ — объем, занимаемый газом при температуре T ₂ и давлении p ₁ (точка 3 на графике).

На участке 3—1 газ отдает количество теплоты Q ₂, равное

Q ₂= Q _3-1= C_p 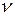(T ₂ – T ₁),

где C_p — молярная теплоемкость газа при изобарном процессе.

Подставим найденные значения Q ₁ и Q ₂ в формулу (1):

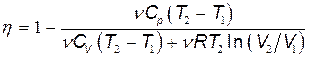
В полученном выражении заменим отношение объемов V ₂/ V ₁, согласно закону Гей-Люссака, отношением температур (V ₂/ V ₁= T ₂/ T ₁) и зная C _v и C_p для двухатомного газа [ C _v=5 R /2, C _p =7 R /2]. Тогда после сокращения на 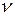и R /2получим

.

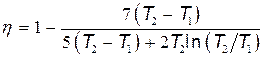Подставив значения T ₁, T ₂ и R и произведя вычисления, найдем

.

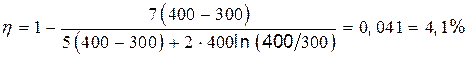Пример 10. В цилиндре под поршнем находится водород массой m =0,02 кг при температуре T ₁=300K. Водород начал расширяться адиабатно, увеличив свой объем в пять раз, а затем был сжат изотермически, причем объем газа уменьшился в пять раз. Найти температуру Т ₂, в конце адиабатного расширения и работу А, совершенную газом. Изобразить процесс графически.

Решение. Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением

,

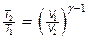где g — показатель адиабаты (для водорода как двухатомного газа g =1,4).

Отсюда получаем выражение для конечной температуры T ₂:

.

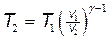Подставляя числовые значения заданных величин, находим

.

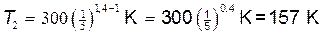Работа A ₁ газа при адиабатном расширении определяется по формуле

.

Подставив сюда числовые значения величин, после вычисления получим

.

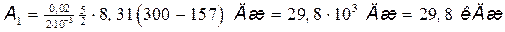Работа A ₂ газа при изотермическом сжатии выражается формулой

A₂=RT₂(m/M)ln(V₁/V₂).

Произведя вычисления по этой формуле, найдем

A ₂= – 21 кДж.

Знак минус показывает, что при сжатии газа работа совершена внешними силами.

Общая работа, совершенная газом при рассмотренных процессах, А = A ₁+ A ₂=29,8кДж + (–21 кДж) =8,8 кДж.

График процесса приведен на рис. 22.

Пример 11. Нагреватель тепловой машины, работающей по обратимому циклу Карно, имеет температуру t ₁=200°С. Определить температуру Т ₂, охладителя, если при получении от нагревателя количества теплоты Q ₁= 1 Дж машина совершает работу A=0,4 Дж? Потери на трение и теплоотдачу не учитывать.

Решение. Температуру охладителя найдем, использовав выражение для термического КПД машины, работающей по циклу Карно, h =(T ₁ – T ₂)/ T ₁. Отсюда

T ₂ = T ₁(1 – h). (1)

Термический КПД тепловой машины выражает отношение количества теплоты, которое превращено в механическую работу A, к количеству теплоты Q ₁, которое получено рабочим телом тепловой машины из внешней среды (от нагревателя), т. е. h = A/Q ₁. Подставив это выражение в формулу (1), найдем

T ₂= T ₁(1 – A/Q). (2)

Учтя, что T ₁=473 К, после вычисления по формуле (2) получим T ₂=284 К.

Пример 12. Найти изменение D S энтропии при нагревании воды массой m =100 г от температуры t ₁=0°C до температуры t ₂=100 °С и последующем превращении воды в пар той же температуры.

Решение. Найдем отдельно изменение энтропии D S ' при нагревании воды и изменение энтропии D S " при превращении ее в пар. Полное изменение энтропии выразится суммой D S ' и D S ".

Как известно, изменение энтропии выражается общей формулой

(1)

При бесконечно малом изменении dT температуры нагреваемого тела затрачивается количество теплоты 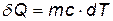, где m — масса тела; с — его удельная теплоемкость. Подставив выражение 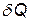в равенство (1), найдем формулу для вычисления изменения энтропии при нагревании воды:

Дата добавления: 2015-03-29