Пример 3.27

Результат — на рис. 3.36.

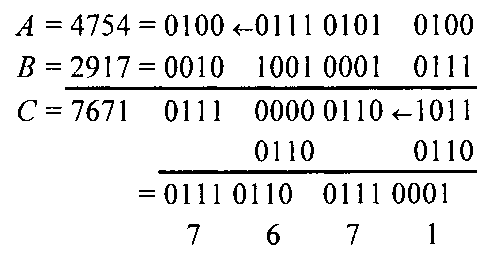
Рис. 3.36. Результат выполнения примера 3.27

Рассмотрим еще один пример арифметического сложения в коде "8421".

Пример 3.28

Результат — на рис. 3.37.

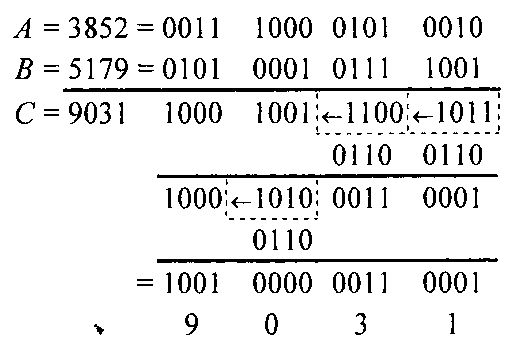
Рис. 3.37. Результат выполнения примера 3.28

Из примера 3.28 видно, что межтетрадные переносы, возникающие в процессе коррекции предварительной суммы, могут таким образом изменить старшие тетрады, что их также потребуется корректировать. В худшем случае количество последовательных коррекций будет равно разрядности слагаемых (рассмотрите пример сложения 9999+1 в коде "8421").

На основании вышеизложенного можно отметить следующие недостатки применения кода "8421":

□ необходимо отслеживать не только переносы из тетрад, но и значения модулей тетрад предварительной суммы;

□ в общем случае невозможно произвести одновременно коррекцию во всех тетрадах, где может потребоваться коррекция.

Для преодоления отмеченных выше недостатков можно использовать другие коды, например "8421+3". При кодировании с избытком три каждая десятичная цифра представляется как 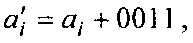где a_i — код "8421" цифры.

Тогда при сложении

(3.32)

где c^h — предварительная сумма, в тетраде всегда будет формироваться истинное значение десятичного переноса — для всех комбинаций десятичных слагаемых, для которых значение 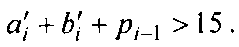. Однако если переноса из тетрады не было, то результат сформируется "с избытком 6", поэтому потребуется коррекция тетрады предварительной суммы — удаление из тетрады лишней тройки. Вычитание (-3) можно заменить сложением с дополнением до 3 — (+13). Обязательно возникающий при этом перенос не передается в следующую тетраду. Потеря переноса равносильно потере 16, т. е.-16+13= -3.

Если перенос из тетрады был, то его вес равен 2⁴=16, таким образом, из тетрады удаляется 16, а вес десятичного переноса — 10. Поэтому перенос из тетрады в коде "8421+3" уносит из тетрады лишнюю шестерку, которую и нужно добавить при коррекции. Но согласно (3.32) сложение тетрад "с избытком 3" приводит к получению суммы "с избытком 6", поэтому вместо добавления шестерки достаточно добавить тройку.

Итак, коррекции при сложении в коде "8421+3" подлежат все тетрады предварительной суммы, причем к тем тетрадам, из которых сформировался перенос, следует добавить константу 0011, а к тетрадам, из которых не было переноса, добавить константу 1101. Возникающие при коррекции межтетрадные переносы игнорируются!

Таким образом, коррекция при сложении в коде "8421+3", во-первых, определяется только значениями переносов из тетрад предварительной суммы и, во-вторых, может проводиться параллельно во всех тетрадах.

Пример 3.29

Результат — на рис. 3.38.

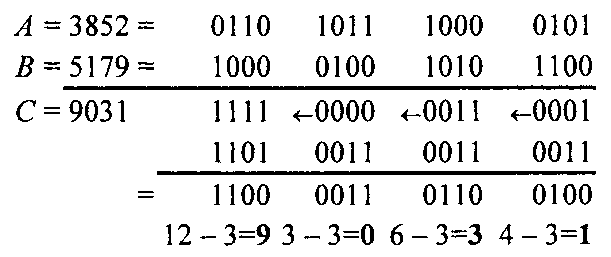
Рис, 338. Результат выполнения примера 3.29

Еще одним достоинством кода "8421+3" является простой способ получения дополнения до 9 — достаточно просто проинвертировать разряды кода.

Действительно, проинвертировав все разряды четырехразрядного двоичного числа а, мы получим его дополнение до 1111=15₁₀, что в коде "с избытком 3" соответствует 15 - (а+3)=(9 - а) +3.

Это свойство позволяет довольно просто реализовать операцию вычитания через сложение в обратном или дополнительном коде.

Дата добавления: 2015-04-25