Дискретизация, квантование, кодирование

Аналоговый сигнал является непрерывной функцией времени, в АЦП он преобразуется в последовательность цифровых значений. Сам процесс преобразования включает в себя три основные операции: дискретизацию, квантование и кодирование (рис. 6.2).

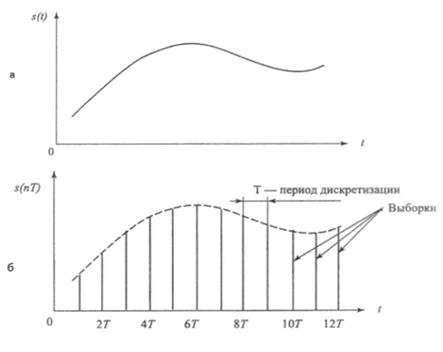
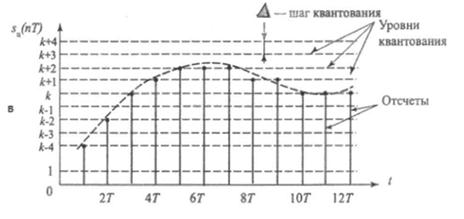
Рис. 6.2. Аналогово-цифровое преобразование: (а) – исходный аналоговый сигнал; (б) – дискретизация; (в) – квантование

Операция дискретизации состоит в том, что по заданному аналоговому сигналу s(t) (рис. 6.2,а) строится дискретный сигнал S(nT), причем S(nT)=S(t). Физически такая операция эквивалентна мгновенной фиксации выборки из непрерывного сигнала S(t) в моменты времени t=nT, после чего образуется последовательность выборочных значений {S(nT)}. Конечно, такую дискретизацию на практике осуществить невозможно. Реальные устройства, запоминающие значения аналогового сигнала (они называются устройствами выборки и хранения – УВХ), не в состоянии сделать этого мгновенно, время подключения их к источнику сигнала всегда конечно. Кроме того, из-за неидеальности ключей и цепей заряда запоминающей емкости УВХ, значение взятой выборки S(nT) в той или иной степени отличаются от величины исходного сигнала S(t). Тем не менее, в абстрактных рассуждениях равенство S(t)=S(nT) считается справедливым.

Поскольку дискретный сигнал S(nT) в моменты времени t=nT сохраняет информацию об аналоговом сигнале S(t) и в спектре сигнала S(nT) содержится спектр сигнала S(t), то последний, очевидно, может быть восстановлен. Для этого дискретный сигнал достаточно пропустить через фильтр низких частот, полоса которого соответствует полосе частот исходного сигнала.

Условие, при котором восстановление исходного сигнала S(t) по его дискретным значениям S(nT) будет возможным, сформулировано в известной теореме Котельникова (теорема отсчетов): если наивысшая частота в спектре функции S(t) меньше f_max, то функция S(t) полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более чем на 1/f_max секунд. Другими словами, чтобы восстановление было точным, частота дискретизации F должна по меньшей мере в два раза превышать максимальную частоту f_max в спектре преобразуемого аналогового сигнала S(t). Эта предельно допустимая максимальная частота f_max в спектре сигнала называется частотой Найквиста f_Н. Нередко частоту Найквиста путают со скоростью Найквиста, которая характеризует минимально возможную для данной частоты Найквиста скорость дискретизации аналогового сигнала и которая вдвое выше максимальной частоты в его спектре (частоты Найквиста).

На практике при дискретизации широкополосных сигналов приходится жестко ограничивать их спектры с помощью высокодобротных фильтров низких частот, которые называются анти-элайсинг фильтрами. Спад характеристики у таких фильтров (как впрочем, и у любых других фильтров) не бывает строго вертикальным. Поэтому реально частота f_max должна быть несколько ниже частоты Найквиста f_Н. Тем не менее, при анализе теоретических моделей аналого-цифровых преобразователей часто пользуются понятиями частоты и скорости Найквиста, полагая, что скорость Найквиста F_Н – это удвоенная частота Найквиста f_Н, т.е. F_Н=2f_Н. В подавляющем большинстве случаев используется равномерная (с постоянным периодом) дискретизация – как по причине того, что к ней легче применить математический аппарат, так и по причине того, что устройства для ее осуществления гораздо проще реализовать физически.

После того, как сигнал дискретизован, производится его квантование и кодирование, что, собственно, является основной операцией при аналого-цифровом преобразовании. На этом этапе по заданному дискретному сигналу S(nT) строится цифровой кодированный сигнал S_ц(nT). Так же, как и дискретный, цифровой сигнал описывается решетчатой функцией, но в данном случае эта решетчатая функция является еще и квантованной, т.е. способной принимать лишь ряд дискретных значений, которые называются уровнями квантования (рис. 6.2,в). Уровни квантования образуются путем разбиения всего диапазона, в котором изменяется аналоговый сигнал на ряд участков, каждому из которых присваивается определенный номер. Эти номера кодируются заранее выбранным кодом, чаще всего двоичным, а их число N выбирается равным 2^m, где m – разрядность кода.

Если сигнал однополярный, то все 2^m уровней будут выражать положительные значения аналогового сигнала, для двухполярного одна половина (2m/2=2^m-1) уровней будет выражать отрицательные значения сигнала, другая (также 2^m-1) – положительные.

Квантование может осуществляться двумя способами. При одном способе расстояние между любыми двумя соседними уровнями, которое называется шагом квантования, будет одинаковым (так называемое линейное квантование). Способ, когда шаг квантования изменяется, это нелинейное квантование. В дальнейшем будут рассмотрены линейные АЦП.

Дискретные сигналы, как и аналоговые, образуют линейное пространство относительно операций сложения, вычитания, умножения, если выполняется условие теоремы Котельникова. Цифровые же сигналы, полученные путем квантования, линейного пространства относительно операций сложения и умножения не образуют. Во-первых, процедура квантования почти всегда сопровождается появлением неустранимой погрешности. Во-вторых, линейная комбинация цифровых сигналов, выражаемых m-разрядными кодами, может иметь разрядность большую, чем m (особенно при операциях умножения), чтобы получить m-разрядный код результата, приходится выполнять операцию округления и усечения. Поэтому устройства цифровой обработки сигналов, реализующие преобразование одной цифровой последовательности S_ц(nT) в другую S_ц(nT) путем выполнения обычных арифметических операций сложения и умножения (в САУ обычно расчет регуляторов), являются нелинейными.

Часто при проектировании систем, включающих в себя устройства аналого-цифрового и цифро-аналогового преобразований сигналов, полученных в результате ограничения спектра широкополосных сигналов с помощью фильтров низких частот, разработчики переносят утверждение теоремы Котельникова о возможности точного восстановления исходного аналогового сигнала по отсчетам дискретного на результат аналого-цифрового и цифро-аналогового преобразований, что является ошибочным. Поэтому в том виде, в котором теорема Котельникова сформулирована для дискретных сигналов, к системам, включающим в себя АЦП- и ЦАП-преобразования, неприменима, она может служить только теоретической моделью для очень приблизительных расчетов.

Поскольку реальные АЦП не могут произвести аналого-цифровое преобразование мгновенно, входное аналоговое значение должно удерживаться постоянным, по крайней мере от начала до конца процесса преобразования (этот интервал времени называют временем преобразования).

В настоящее время выпускается большее число интегральных АЦП, которые отличаются конструктивной и функциональной закономерностью, но в основу работы заложены некоторые стандартные, фундаментальные принципы. При этом в структуре некоторых АЦП присутствует устройство УВХ, в других УВХ отсутствует.

Дата добавления: 2015-03-29