Пример 2-8 Проецирование в однородных координатах

Для отрезка АВ из рис. 2-14 имеем р = q = 1, [ А ]= [1 3 1] и [ В ]= [4 1 1],

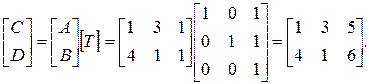
Таким образом, [ С ]= [1 3 5] и [ D ]= [4 1 6] на плоскости h=x+y+ 1. Проецируя обратно на плоскость h = 1 путем деления на коэффициент однородных координат, проведем двумерное преобразование точек

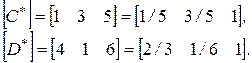
Результат показан на рис. 2-14.

2-19 ПРОПОРЦИОНАЛЬНОЕ МАСШТАБИРОВАНИЕ

Оставшийся необъясненным элемент s (3 х 3)-матрицы преобразования соответствует пропорциональному масштабированию, при котором все компоненты вектора изменяются пропорционально. Покажем это, рассмотрев следующее преобразование:

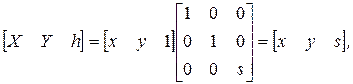(2-58)

где X = x, Y = y и h = s. После нормализации получим X = x/s и Y = у/s. Таким образом, преобразование [ х у 1][ Т ]= [ x/s y/s l] является равномерным масштабированием координатного вектора. Если s < 1, то происходит растяжение, а если s > 1 —сжатие.

Заметим, что это преобразование осуществляетсятакже в плоскости h = 1. Здесь h = s = const, и поэтому плоскость h 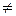1параллельна плоскости h = 1. Геометрическая интерпретация данного эффекта показана на рис. 2-15. Еслиs<1, то h = const задает плоскость, лежащую между плоскостями h = 1 и h = 0. Следовательно, когда преобразуемая прямая АВ проецируется обратнона плоскость h = 1, то А 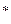В 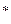увеличивается. Аналогично, если s > 1, то h =const определяет плоскость, расположенную за плоскостью h = 1 и проходящуювдоль оси h. В случае проецирования прямой CD на плоскость h = 1 происходитуменьшение прямой C 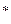D .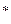

2-20 ТОЧКИ БЕСКОНЕЧНОСТИ

Однородные координаты предоставляют удобный и эффективный способ нанесения точек из одной системы координат в соответствующие точки альтернативнойкоординатной системы. Бесконечная область в одной координатной системе частопреобразуется в конечную область в альтернативной системе. При некорректномвыборе переноса параллельность прямых может не сохраняться. Однако точкипересечения после преобразования оказываются снова в точках пересечения.Данное свойство используется дляопределения однородных координат представленияточек бесконечности.

Рассмотрим пару пересекающихся прямых, заданных уравнениями

.

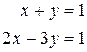Прямые пересекаются в точке скоординатами х = 3/5, у = 2/5. Запишем уравненияв виде x+y - 1 = 0, 2 х – 3 y = 0 и представим их в матричной форме

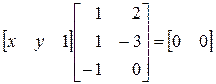
или

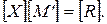
Если матрица [ M' ]квадратная, то пересечение может быть получено путем обращения матрицы. Изменим систему исходных уравнений следующим образом:

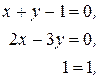
или в матричной форме

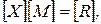
т.е.

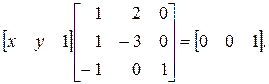
Квадратная матрица, обратная данной, имеет следующий вид:

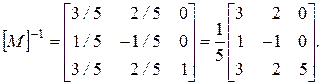
Умножая обе части уравнения на [ М ]^-1и учитывая, что [ М ][ М ]^-1= [ I ]является тождественной матрицей, получим

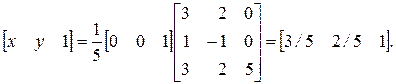
Таким образом, точка пересечения опять имеет координаты х = 3/5, у = 2/5.

Рассмотрим теперь две параллельные прямые, заданные следующим образом

По определению геометрии Евклида, точка пересечения двух параллельных прямых расположена в бесконечности. Продолжая предыдущие рассуждения, вычислим точку пересечения этих прямых, заданных в матричной форме,

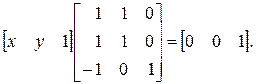
Однако несмотря на то что матрица квадратная, она не имеет обратной, так как две ее строки тождественны. Такая матрица называется сингулярной. Возможна иная формулировка с обратимой матрицей. Получим ее, переписывая систему уравнений следующим образом:

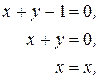
или в матричной форме

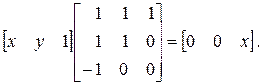
В данном случае матрица не является сингулярной и существует обратная ей

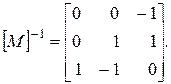
Умножая обе части выражения на обратную матрицу, получаем

.

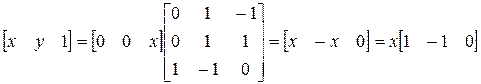Результирующие однородные координаты [1 -1 0] определяют точку пересечения двух параллельных прямых, т.е. точку бесконечности. В частности, они представляют данную точку в направлении [1 -1] двумерного пространства. В общем виде двумерный координатный вектор [ а b 0] представляет точку бесконечности на прямой ау - bх = 0. Приведем несколько примеров:

[ 1 0 0] точка на положительной оси x,

[-1 0 0] точка на отрицательной оси х,

[ 0 1 0] точка на положительной оси у,

[ 0 -1 0] точка на отрицательной оси у,

[ 1 1 0] вдоль прямой у = х в направлении [1 1].

Таблица 2-1 Однородные

координаты для точки [4 3]

h x* y* X Y

1 4 3 4 3

1/2 8 6 4 3

1/3 12 9 4 3

:

1/10 40 30 4 3

:

1/100 400 300 4 3

:

Вектор с однородной компонентой h = 0 действительно представляет точку бесконечности и может быть также интерпретирован как движение к пределу (табл. 2-1).

Рассмотрим прямую у 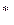= (3/4) х 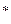и точку [ X Y h ] = [4 3 1]. Напомним, что в однородных координатах не существует единственного представления координатного вектора (табл. 2-1). Точка [4 3 1] представлена в однородных координатах по всем направлениям. Заметим, что в этой таблице при h 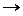0 отношение y 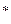/ x 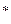остается равным 3/4, как и требуется длясохранения уравнения.Кроме этого, обратим внимание на то, что следующая пара (x 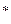y 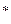), все точки которой располагаются на линии у 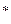= (3/4) x 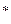, быстро приближается к бесконечности. Таким образом, предел при h 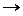0 и есть точка бесконечности, заданная в однородных координатах как [ X Y h ]= [4 3 0].

Обратившись снова к рис. 2-15, легко продемонстрировать геометрическую интерпретацию процесса движения к пределу при h 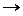0. Рассмотрим отрезок единичной длины, проходящий от точки начала координат в направлении [1 0] на плоскости h = s (s < 1). При s 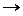0 проекция этой прямой обратно на физическую плоскость h= 1 в направлении лучей, проходящих через начало координат, становится бесконечной длины. Следовательно, конечная точка прямой должна представляться точкой бесконечности на оси X.

2-21 ПРАВИЛА ВЫПОЛНЕНИЯ ПРЕОБРАЗОВАНИЙ

Для представления данных и выполнения преобразований с помощью умножения матриц используются различные соглашения. Наибольшее внимание нужно уделять формулировке задач и интерпретации результатов. Например, перед выполнением поворота необходимо получить ответы на следующие вопросы.

В правосторонней или левосторонней системе координат определяются поворачиваемые координатные векторы?

Вращается объект или система координат?

Как определяются положительный и отрицательный повороты?

Координаты записываются в виде строки или столбца матрицы?

Вокруг какой линии или оси осуществляется поворот?

В данном изложении используется правосторонняя система координат, объект вращается в неподвижной координатной системе, положительный поворот определяется правилом правой руки, т. е. поворот по часовой стрелке осуществляется вокруг оси при наблюдении от начала вдоль положительной оси, и координатные векторы представляются в виде строки матрицы.

Выражение (2-29) задает преобразование для положительного поворота вокруг начала координат или оси z. Так как вектор задается строкой матрицы, то матрицу преобразования следует разместить после данных или матрицы координатных векторов. Это преобразование задается путем умножения справа. В случае однородных координат для положительного поворота объекта на угол q вокруг начала координат (оси z) использование умножения справа приводит к следующему результату:

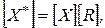
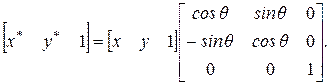(2-59)

Если мы подставим координатные векторы, заданные в однородных координатах в виде столбца матрицы, то поворот можно выполнить следующим образом:

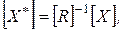
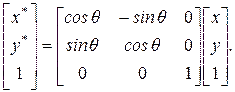(2-60)

Выражение (2-60) называется преобразованием с умножением слева, так как матрицапреобразования расположена перед столбцом координатного вектора или данных.

Заметим, что (3 х 3)-матрица в выражении (2-60) есть транспозиция (3 х 3)-матрицыиз выражения (2-59). Это свидетельствует о независимости строк и столбцовматрицы.

Длятого чтобы повернуть систему координат и оставить неизмененными координатныевекторы, необходимо в выражении (2-59) заменить q на - q. Вспомним, что sinq = - sin (-q), a cosq = cos (- q).

Теперь выражение (2-59) будет иметь вид

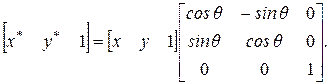(2-61)

Рис. 2-16 Эквивалентность преобразования координатных векторов и систем координат.

Заметим, что (3 х 3) матрица опятьимеет обратную и также транспонируется в матрицу из (2-59).

Если вращается система координати используется левосторонняя координатная система, то замену 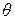на 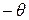надопроизводить дважды, а уравнение (2-59) снова оказывается справедливымпри допущении, что применяется последующее умножение на строку матрицыданных.

Заметим, что, как показано нарис. 2-16, вращение против часовой стрелки векторов, задающих объект, идентичноповороту в том же направлении координатных осей при неподвижномобъекте. Опять нет необходимости в изменении содержимого матрицы преобразования 3x3, если нет других причин для ее редактирования. Эти несколькопримеров показывают, насколько аккуратно необходимо выполнять матричныепреобразования.

Дата добавления: 2015-04-25