Пример 3-1 Комбинированное преобразование

Рассмотрим пример более сложного преобразования, которое мы представим в виде последовательности элементарных преобразований. Пусть требуется построить матрицу M вращения пространства на угол 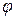вокруг прямой L, проходящей через точку A(a,b,c) и имеющей единичный направляющий вектор (l,n,0), то есть параллельный плоскости XY (рис. 3-1).

Задача сводится к последовательному применению следующих элементарных преобразований:

· сделаем так, чтобы прямая L проходила через начало координат. Для этого надо осуществить перенос пространства на вектор –A=(-a, -b, -c). Соответствующая матрица преобразования имеет вид:

.

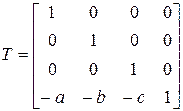· совместим прямую L с осью Y. Для этого выполним поворот пространства на угол 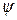(который надо еще вычислить) вокруг оси Z. Зная направляющий вектор (l, n, 0) прямой L, получаем для угла 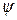: 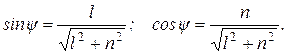Соответствующая матрица имеет вид:

.

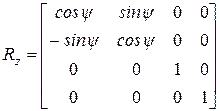· повернем пространство на угол 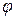вокруг прямой L. Так как теперь прямая L совпадает с осью Y, то это будет поворот вокруг оси Y и соответствующая матрица (см. 3-3) будет следующей:

.

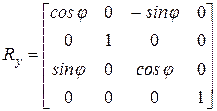· восстановим исходное направление прямой L. Для этого выполним поворот на угол 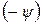вокруг оси Z. Матрица преобразования будет обратной к матрице R_z и получается из нее заменой угл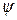а на 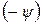. Отсюда получаем:

.

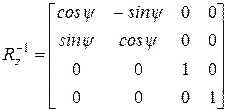· восстановим исходное положение прямой L. Для этого осуществим перенос на вектор A=(a, b, c). Соответствующая матрица T^-1 будет обратной к матрице T:

.

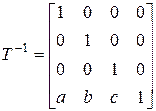Окончательная матрица заданного преобразования будет равна произведению матриц использованных элементарных преобразований, то есть 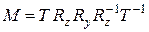. Например, при

При произвольных параметрах получается довольно громоздкое выражение.

ЛИТЕРАТУРА

1. Роджерс Д., Адамс Дж. Математические основы машинной графики/Пер. с англ.-М.: Машиностроение,2000.-240с.

2. Воеводин В.В. Линейная алгебра/-М.:Наука, 1980.

3. Курош А.Г. Курс высшей алгебры/-М.: 1962.

Содержание

1. Обзор машинной графики. 3

1-1 ВВЕДЕНИЕ.. 3

1-2 ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ.. 3

1-3 ПОДГОТОВКА ИЗОБРАЖЕНИЙ ДЛЯ ВЫВОДА.. 4

1-4 ПРЕДСТАВЛЕНИЕ ПРЕДВАРИТЕЛЬНО ПОДГОТОВЛЕННОГО ИЗОБРАЖЕНИЯ.. 5

2 Двумерные преобразования. 9

2-1 ВВЕДЕНИЕ.. 9

2-2 ИЗОБРАЖЕНИЕ ТОЧЕК.. 9

2-3 ПРЕОБРАЗОВАНИЯ И МАТРИЦЫ... 9

2-4 ПРЕОБРАЗОВАНИЕ ТОЧЕК.. 10

2-5 ПРЕОБРАЗОВАНИЕ ПРЯМЫХ ЛИНИЙ.. 12

2-6 ПРЕОБРАЗОВАНИЕСРЕДНЕЙ ТОЧКИ.. 13

Пример 2-1 Средняя точка прямой. 14

2-7 ПРЕОБРАЗОВАНИЕ ПАРАЛЛЕЛЬНЫХ ЛИНИЙ.. 15

2-8 ПРЕОБРАЗОВАНИЕ ПЕРЕСЕКАЮЩИХСЯ ПРЯМЫХ.. 15

Пример 2-2 Пересекающиеся прямые. 18

2-9 ПОВОРОТ. 19

2-10 ОТРАЖЕНИЕ.. 21

Пример 2-3 Отражение и вращение. 23

2-11 МАСШТАБИРОВАНИЕ.. 24

Пример 2-4 Комбинированные преобразования на плоскости. 27

2-13 ПРЕОБРАЗОВАНИЕ ЕДИНИЧНОГО КВАДРАТА.. 28

Пример 2-5 Масштабирование области. 29

2-14 ПРЕОБРАЗОВАНИЕ ЖЕСТКИХ КОНСТРУКЦИЙ.. 30

2-15 ПЕРЕМЕЩЕНИЯ И ОДНОРОДНЫЕ КООРДИНАТЫ... 32

2-16 ПОВОРОТ ВОКРУГ ПРОИЗВОЛЬНОЙ ТОЧКИ.. 32

Пример 2-6 Поворот относительно произвольной точки. 33

2-17 ОТРАЖЕНИЕ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ПРЯМОЙ.. 34

Пример 2-7 Отражение относительно произвольной прямой. 34

2-18 ПРОЕЦИРОВАНИЕ-ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ОДНОРОДНЫХ КООРДИНАТ. 36

Пример 2-8 Проецирование в однородных координатах. 37

2-19 ПРОПОРЦИОНАЛЬНОЕ МАСШТАБИРОВАНИЕ.. 38

2-20 ТОЧКИ БЕСКОНЕЧНОСТИ.. 39

2-21 ПРАВИЛА ВЫПОЛНЕНИЯ ПРЕОБРАЗОВАНИЙ.. 41

3 Трехмерные преобразования. 43

3-1 ВВЕДЕНИЕ.. 43

3-2 ПОВОРОТЫ ВОКРУГ ОСЕЙ.. 43

3-3 РАСТЯЖЕНИЕ ВДОЛЬ ОСЕЙ.. 44

3-4 ОТРАЖЕНИЕ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ.. 44

3-5 Перенос (сдвиг) 45

Пример 3-1 Комбинированное преобразование. 45

ЛИТЕРАТУРА.. 46

Дата добавления: 2015-04-25